|
Is selection of genes or individuals? How does large-scale gene flow work? How can we explain the evolution of sex? What is the smart gene hypothesis? |
|
|
Neo-Darwinist, homologous, orthologous, paralogous, eukaryotic, prokaryotic, selfish gene, smart gene, sexual reproduction, genome, spectrum, probability, DNA, RNA |
|
|
Return to the Theory of Options |
|
|
Previous 2.3 Phylogenic Evolution |
|
Hey! If you actually found this page, it is slightly out of date. There is a shorter, updated version at
equation.htm or model.pdf. Basically, this theory says that the equations of large-scale evolution must be solved using complex numbers (root -1). If you are interested in this, email me at [email protected].2.4 The Heuristic Process
"But multitudinous atoms, swept along in multitudinous courses through infinite time by mutual clashes of their own weight, have come together in every possible way and realized everything that could be formed by their combinations. So it comes about in a voyage of immense duration in which they have experienced every variety and movement of conjunction, has brought together those whose sudden encounter normally forms the starting point of substantial fabrics - earth and sea and sky and the races of living creatures." Lucretius.
"The chance that a functioning cell could evolve in that time can be likened to the probability that a tornado sweeping through a junkyard might assemble a Boeing 747." Sir Fredrick Hoyle
"If black moths can replace white moths in a century, then reptiles can become birds in a few million years by the smooth and sequential summation of countless changes. The shift in gene frequencies is an adequate model for all evolutionary process -or so the current orthodoxy states." Steven Jay Gould
"Because of the excellence of his essays, (Steven Jay Gould) has come to be seen by non-biologists as the preeminent evolutionary theorist. In contrast, the evolutionary biologists with whom I have discussed his work tend to see him as a man whose ideas are so confused as to be hardly worth bothering with, but as one who should not be publicly criticized because he is at least on our side against the creationists." John Maynard Smith.
"Together, these two processes ... (random genetic drift and natural selection) ... work to mold the genetic constitution of future generations and, ultimately, species, often acting in the same individual. For example, when a child dies from a genetic disease, all the child's genes which do not affect the outcome of the disease will suffer a chance death." Majerus, Amos, Hurst, 'Evolution - The Four Billion Year War'
"Eleazar begat Phinehas, Phinehas begat Abishua, And Abishua begat Bukki, and Bukki begat Uzzi, And Uzzi begat Zerahiah, and Zerahiah begat Meraioth, Meraioth begat Amariah, and Amariah begat Ahitub, And Ahitub begat Zadok, and Zadok begat Ahimaaz, And Ahimaaz begat Azariah, and Azariah begat Johanan." Chronicles
"That one body may act upon another at a distance through a vacuum, without the mediation of anything else, by and through which their actions and force may be conveyed from one to another, is to me so great an absurdity, that I believe no man, who has in philosophical matters a competent faculty of thinking, can ever fall into it." Isaac Newton.
"Even worse is the mathematical concept of imaginary time... I was savagely attacked by a philosopher of science for talking about imaginary time. He said: How can a mathematical trick like imaginary time have anything to do with the real universe? I think this philosopher was confusing the technical mathematical terms real and imaginary numbers with the way that real and imaginary are used in everyday language." Steven Hawking
"The universe is not only queerer than we suppose, but queerer than we can suppose." J. B. S. Haldane.
2.4.1 Models of Gene Flow
Whatever occurs in evolution or life, however we explain it, no one, theist or atheist, wants to be alarmed by processes that we do not understand. We know that natural processes will be complex, but we hope that they can be explained in everyday terms. An object cannot exist in two places at once. Simultaneous events cannot occur at different times, and objects cannot alter other objects without physical events connecting them.
Scientifically, we learn about such strange events not so much directly, but via the symbolic proofs of mathematics. Data first appears to us in ways that do not make everyday sense. Then somebody proves that no matter how strange the data seems, there is a mathematical reason why it might appear that way. This only proves, really, that we have no logical grounds for saying the data should not be this way, rather than explaining it. Yet, proving the mathematically consistency of how facts appear is unsurpassed at conviction. A person can have a theory of punctuated change, selfish DNA, or another effect. Yet, even if we thought such a theory was absurd, we could not claim it was not logical if an equation can show that it is. So, despite that Darwin's original theory was remarkably free from math, the push is now on to prove by equations the self-consistency of all these ideas.
What are these equations?
Well, all equations of evolution begin from a binomial equality;
(p + q)2 = p2 +q2 +2pq
This equality explains the distribution between diploid alleles, p and q, in a large, stable, population. (Diploid is if one gene from a pair is expressed at a locus. In sexual reproduction, mostly each parent contributes one gene.) The above equation is used to calculate the chances of couples with a rare disease having an affected child, or the distribution of a harmful gene in a population. Only evolution is not about populations in equilibrium, but how they change over time, so the equation is modified. Roughly, any individual composes a collection of alleles and genes, denoted xi, where i = 1, 2, 3 in a series. Any gene xi can mutate to a new type at any time t. So, if the new mutation has fitness wi, greater than average fitness <w>, we want to know how fast the new gene will spread. The diploid case is complex, but a simpler result for a haploid (only one gene per locus) would be;
D xi (t) = xi (t) [wi (t) - <w> (t)]/ <w> (t), where <w> is mean fitness
and
<w> (t) = S xi (t) wi (t), i = 1, 2, 3…
The first equation It says that spread of xi will depend on how fitter wi, the new gene makes the individual above mean fitness <w>. (The fitter the individual, the greater will be wi - <w>, so the faster its genes spread, until <w> itself rises to the level of wi.) The second equation says that <w> is the sum of the fitness components of an average individual.
Are these equations correct?
Well, these equations are simplified forms to give the reader an idea. Actual equations used are horrendously complex. Yet even as simple forms these are equations of real processes. We could not say that they were not "true", but only that they do not model the events claimed. Yet the equations are constantly checked against available data, and mostly they correlate the assumptions. (If say, we assume population size is infinite the equation might not work for small populations, but we allow that.) Again too, the equations do not so really have to explain anything. They only demonstrate that there are no logical grounds for arguing that fitness would not act that way. If we are still not convinced we must produce our own equations, showing how the fitness really would act.
Even so, there are many controversies over these equations. The first equation is often called the fundamental theorem of natural selection. We need not take this title literally, but the equation does infer that mean fitness can only rise. But this depends on the terms. Mean fitness will rise if we take it as a relative measure of fitness at the time. Only while a population will increase mean relative fitness to adapt at that time, absolute fitness can still fall, if we measure this as total exact copy of DNA passed on over time. This happens in sex. (Sexual reproduction is diploid, but the fundamental theorem applies.) Asexual organisms evolved first and copy 100% of an individual's DNA into the next generation. Sexually reproducing organisms evolved later, but copy only 50% parent DNA to the child. 50% is a huge loss, especially as populations can switch to haplodiploidy to get 75% fitness, or to asexual reproduction and get 100% transmission. But few populations do this, and then for other reasons. This anomaly of why over time fitness fell for reproduction by sex has never been explained.
Yet, while sex is the best-known example of it, exact copy fitness must have fallen for many large changes. Eukaryotic cells are a hundred times more complex than prokaryotic ones, have more unexpressed or non-coded DNA, and propagate in far lesser numbers. Prokaryotic cells of the types around when eukaryotic life evolved could most likely copy 100% of DNA exactly into billions of subsequent generations, copy profligacy the simplest eukaryotic cell could not match. Multi-celled organisms would also copy less exactly and profusely than single celled ones, for similar reasons. Yet, both these complex life forms evolved from simpler, more easily copied ones, at what must have been a large fitness cost.

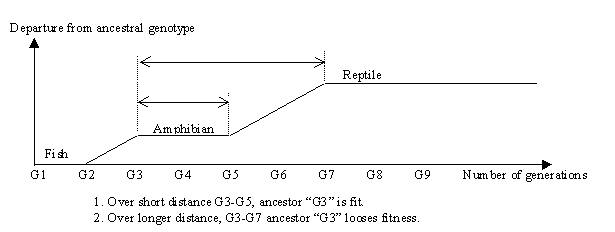
We like to think that types "higher" up the scale of life are fitter. This might not be the case if we measure fitness strictly by exact copy of genome. The founding amphibian and founding reptile were fit for that line, but each founder diverged far from the genome of an original type, to found a new line.
The loss of fitness is the "cost" to evolve. We could measure this many ways, such as increased metabolic rate, complexity of the birth process, or reduced litter size. But the simplest measure is the amount that DNA in a descendent had to vary from the DNA of the ancestor for the lineage to adapt All organisms have a phenotypic urge to reproduce, and the amount of DNA they pass on quantifies how successful they were. But no organism cares for the measure as motive. Humans would not exchange their life style with a simpler organism, despite that by choice some humans do not pass on DNA. Difference in relative fitness quantifies pressure to adapt, and absolute copy fidelity quantifies the 'distance’ any initial design had to alter to adapt, which is always at a cost. Sex is a problem only because it has been noticed, but we should find that fitness falls any time major complexity evolves a large genome distance from where it was before.
2.4.2 Time and Change
Still, if absolute fitness falls as species become more complex, how do we reconcile this with equations showing that fitness only rises?
Well, all equations of evolution relate fitness of the gene directly to the fitness of the organism. But this might not be correct. Genes of course, are only selected while resident in living, reproducing organisms (mostly). Yet organisms live and die in an evolutionary instant, while genes persist for huge periods, billion of times as long. The ratio of difference by which a base pair (bp) of DNA alters per generation over a gene and a genome is huge. Some genes have only altered one bp in 1013 generations, almost the history of life. But DNA in a modern genome might mutate 100 bp every gamete, each time reproduction is attempted. This is a 1015 ratio of difference in rate of change between a gene and genome. We need to check if over such a huge ratio, the gene and genome have the same criteria of fitness.
Although the convention seems strange, the best way to quantify huge ratios is via a trigonometric angle, we will call q (theta). As ratios become small, once per gamete or 100 times per gamete (100 or 10-2) we adjust the angle such that q ® 00 (theta goes to zero degrees). If ratios are huge, once per 1013 or 1014 generations, or forever, q ® 900 (to 90 degrees). We must set a median rate, which is controversial, but let us take the average mutation rate of genes as one bp per gene every 107 generations, to give q » 450 as an approximation. We can now describe any interval of time, from the tiniest instant to forever on a single diagram, as shown below.
|
|
If we label permanence in time as an angle, all instantaneous events occur along the horizontal axis. Events less affected by time 'rotate' into higher angles. 'Forever' will be a vertical line rotated 900 from the horizontal. This way we can picture "all of time" within a single frame of it. |
Using the diagram, how do genes behave over the history of life?
Well, they always seem to 'rotate' counterclockwise (CCW) from a flat angle, q = 00, to a higher angle, q >00 (is greater than). If the gene does not mutate it will rotate steadily, from q = 00 when it began, for however long the gene then exists. The enzyme sequence AYQGFA does not change over life. So AYQGFA evolved first at q = 00, then rotated steadily CCW for however long life existed. And this is how most genes evolve. Average mutation rate is one in 107 generations, but other averages are at 108 or 109 generations. There are molecular reasons genes alter at these rates, but there were also 'explosions' of new orders, classes, and phyla, those generations ago in the past. Plus once they radiate many genes become "frozen" beyond that point, because any alteration would disrupt the underlying homology of the new order, class or phyla. Once a new homology evolves, there are further 'sub-explosions' of new families and species. This produces new genes, but at shorter generation times (106 for a family or 105 for a species). These genes too begin from q = 00, but they will not 'rotate' as far in the short generation times over which the newer combinations exist.
Even so, for an agreed rate, mutation will slow or decrease rotation, so many genes do this. Plus genes do not evolve new at q = 00, but many break or split from existing genes into functional or non-functional pairs. Selection will tend to hold functional genes at high angles. But loss of selection allows non-function genes or DNA segments sink or regress, falling back clockwise (CW) to lower angles. Plus in modern life the low angle is crowded with virus, non-coded or parasitic genes and DNA. These break from existing sequences and try to replicate into new niches. But as life saturates there is less opportunity for the new forms to rotate to higher angles.
Let us examine how a rotation effect can be described in an equation. Firstly, once we assign each gene, genome or DNA segment an angle, we specify its spread not as a single number (xi) but by a coordinate (xi, q i). It is just algebra, but we can resolve coordinates (xi, q i)t, into a complex form;
F (xi, q i)t = F (a + jb) where j = Ö -1.
Now recall in the equations wi, fitness, affected the gene, xi directly. Yet, w only acts on a whole organism, which is only selected at q = 00. This means that w acts only on the component of genes at q = 00, which is only the 'a' component of the complex term, but not the 'b' one. So, the full fitness sum for <w> would have to be the complex sum;
<w> (t) = S ai (t) wi (t) + jS bi(t), i = 1, 2, 3…
Now at q = 00, ai = xi and bi = 0, which makes the standard equation correct at low angles;
<w> (t) = S xi (t) wi (t), i = 1, 2, 3…
This solves the mystery that if the equations are not correct, why do they work? Simply, the equations work at low angles, which is true, because they work best for host-parasite systems, or rapidly adapting modern organisms, where q under study is at low angles.
Yet, w only acting at q = 00 is another reason genes would 'want' to rotate to higher angles. They try to avoid selection! Any gene at q = 00 faces a selection challenge every generation. It can be wiped out at any time, which happens to genes with low q . But genes with high q do not face this. The H4 gene has altered one bp in 1013 generations, so its q ® 900. Yet this genes has survived the K-T extinction (that killed the dinosaurs) unaltered. Other basic enzyme and RNA sequences exist at such high q that they could be only selected out by global extinction.
Except all genes begin life at q = 00, where the equations are correct, plus they need to spread from this early point as xi dependent on wi. So how does the transformation from low to high q take place? Plus if wi always acts with less effect at q >00, what is the relationship wi to q i?
Well, the exact relationship would have to be calculated using complex numbers, and this has not been done. But a crude relationship is that the gene will maximize its success where b = wa. This shows that maximum fitness, wi = 1, is best for the gene only at angle q i = 450. If true, this would explain why most genes converge at average stability, and are neither exceptionally conserved nor exceptionally unstable.
The next result however, is a bit strange. It shows that if q i < 450 (less than) then it is best for the gene if wi < 1. This infers that if genes are forced to propagate at low q , they do not "care" if the phenotype is fit. Strangely, this is also how genes behave, in that most low q genes or DNA is junk, viral or parasitic, and it does damage hosts. Also, in early life low q genes would be quickly selected out (by being in weak phenotypes). This would tend to drive average q higher quickly, which is another reason why q does tend to drive towards a median for useful genes.
The most surprising result however, is that to achieve q i > 450 requires wi > 1. This is not possible (fitness w cannot exceed 1). We can only explain this by noting, firstly, that genes for which q i > 450 evolved in the deep past. (Even if it did not mutate, a gene must have evolved 107 generations ago to be at 450 today, on our diagram.) In these earlier periods we saw huge build ups of evolutionary pressures, leading to drastic change that we compared to an evolutionary 'supernova', where totally new types evolved the first time. (See previous chapter.) As explained, it was during these periods there must have been huge falls of fitness over many generations, as totally new, far more complex types evolved. Except this only deepens the conundrum, because if the fitness of genes has to rise >1 for genes to spread > 450, why does it have to happen only in a period when genome fitness falls?
This author believes that a full calculation using complex numbers and correlating all the available data would show why it happens. Sex say, exists throughout a Kingdom for maybe 1010 generations, at about of q i = 800. To reach such a high angle requires a wi = 2. In the full calculation this would compensate over the rest of the genome, as a loss of fitness, wk = 0.5, for the genes at lower angles. (Although w is possibly not the best term to use.) Also, remember that even in the new equation, all change still occurs at an instant, q = 00. And at that instant the equation reverts to its standard form and relative (we call it relative) fitness <w> always rises. It is over the whole lineage that absolute fitness of the entire genome will fall.
Even so, the process is difficult to visualize. The effects of the earlier equations were unfamiliar too, until Richard Dawkins coined the metaphor "selfish gene", to crystallize what these equations inferred. Since then it has become more complex, requiring additional metaphors of "outlaw" or "ultra-selfish" to explain the further intent. Plus the "selfish" metaphor should only be used to explain how the math works, not what genes actually do.
Yet allowing for these limitations, is there then a simple metaphor that can show how the new, more complex equations would differ from those equations that led to the "selfish gene" metaphor.
There is. It is called the "smart gene" hypothesis.
2.4.3 "Smart Genes"
The metaphor "smart gene" has one purpose: to explain the difference between an equation using a single value (xi) to specify gene propagation, and one using polar coordinates (xi, q i). The differences occur at high angles of q for individual genes. (At q = 0, the equation reverts to standard form.) Events most studied in evolution, mutation of single genes or adaptation over a few generations, happen at q = 0. It is only events in the past, which we cannot observe, that need calculating at high angles of q . So, "smart gene" theory has nothing to do with IQ, or genes being clever with intent. Nor does the 'smart' meaning bear any relation to other modern 'smart' devices, such as pills, cards, or bombs. Smart genes are not modern but mostly ancient genes that evolved millions, or billions of years in the past.
But the smart metaphor is important. Selfish gene theories tell us that the gene can only propagate via the success of the immediate phenotype in which the gene is ensconced. But this is a poor strategy, because individual lines can terminate at any time. Smart gene theory allows genes to express homologous, hard-to-alter attributes that can radiate into many lines. It is as though in early life some genes realized that there was going to be extinction, disruption, and termination of lines in later life. To hold sequence, spread and avoid genetic (sequence) death, genes would have to be not just "selfish", but "smart". They would have express traits that did not tie them to single lines but would allow a variety of types, even if variety and competition forced other lines into extinction. Outwards from any radiation there is no guarantee which lineage will survive. Just if one family member is in each lineage and lines are varied enough the sequence will survive. This required genes to;
The concept that genes in early life could conspire as a family, radiating into many lines so that some could survive sounds incredible. Yet, it can be easily explained via phenotype selection. There is a cost of change. If an organism can adapt existing genes slightly, without the risks of mutating new genes, it will lower this cost. So, organisms carrying genes that can be easily adapted for a variety of types will spread, and genes spread with them. Over billions of years, genes that provide organisms with easy, low cost ways to adapt radiate into a huge variety of lines. Genes that can only provide limited or specialized options of adaptation will spread less widely. Looking back from the present, it appears as though some genes were ‘smarter’ than others, when formulating the best strategy to spread and survive.
More difficult is the concept of genes forcing variability, but a good example is genes for sex. Any genes that control basic cell machinery such as reproduction enhance organism variability. This allows them to radiate into many types, so they gain fitness for two reasons.
This is why despite that modern genomes suffer a 50% loss of fitness for sex, genes that matured billions of generations in the past gain fitness from sex! Life needs to be varied to survive. The more varied organisms can be the more chance that any random event (like a climate change or asteroid strike) will not kill them all. Sex has unique genes to express each of its variations. But the basic reproductive machinery of sex, like the replication machinery of cells evolved at a single point and radiated through subsequent life.
Only forcing variability also forces a loss of fitness on genomes, but again we can see this by an example. A genome of eukaryotic life copies less exact DNA than prokaryotic life, if for no other reason than it carries more DNA. More DNA means complexity, variety, change, and competition. So eukaryotic genomes are copied less exactly and in fewer numbers than the prokaryotic genomes they evolved from, which is a loss of absolute copy fitness. Yet, eukaryotic cells only carry more DNA because they can pack it tightly by coiling DNA strands on a base of histones, which are required in all eukaryotic life. But because every eukaryotic genome needs them histones gained fitness from the tight DNA packing. So this genes ends up at a very high angle. Or the H4 sequence ends at a high angle q ® 900, in genomes at a low angle q ® 00, full of DNA also at a q ® 00, which is the characteristic of 90% of modern eukaryotic DNA.
The final problem is that the standard equations presume that genes evolve by a form of gene anagenesis, where a gene evolves in one place over time. But while small adaptive changes are at single gene loci, large changes are by gene doubling, or a gene cladogenesis. A gene will duplicate, then while the first gene holds its original function the non-functional duplicate will mutate at the faster rate for non-selected sequences. The duplicate might drift into worse mutations, but it could also drift into a useful mutation, and regain functionality as a new gene. And while we are not certain when this paralogous gene evolution began, like sex, it looks like another smart gene strategy. There is change to alleles, genomes, and DNA, but the genes that set this whole train in motion are not themselves forced to alter sequence, but find new ways to spread.

The globlin superfamily and many other genes evolved by a type of gene cladogenesis, where genes duplicate and then adapt by small point mutations. Current models of gene flow only consider gene anagenesis, where a gene evolves in a single line. Gene anagenesis cannot account for the major step changes in gene evolution.
2.4.4 The Gene Spectrum
Any struggle among genes to express ‘smart’ attributes would produce a skewered spectrum of mutation rates among modern genes. This is another dispute. If probability theory is applied to the standard equations it predicts a so-called molecular clock, that ticks at a mean rate for all genes, about one mutation in 107 generations. (This clock is of a great concern to Creationists who argue that it does not exist.) Still, we can show in the new equations why genes would tend to cluster at q ® 450, which is the 107 rate. But in 'smart' theory, while many genes will cluster around average, only a small number can obtain very low rates at q ® 900, while huge numbers of DNA segments will mutate at fast rates q << 450. This is because being 'smart' is a somewhat exclusive club, plus the idea is to retain your own sequence at high q , but force the low q cost of change onto more recently evolved genes and DNA in the genome. Plus as we saw, to push q > 450 requires wi > 1, which can only occur a limited number of times in the history of life.

Genes form a spectrum of mutation rates, with highly conserved genes existing first, while other, more recently evolved genes must try to increase conservation by radiating into many types. Gene do not actually 'struggle' with intent or select outside of individual organisms. But over huge times, the effect might be better understood as a struggle among genes.
A struggle to obtain high q will not produce a normal distribution of mutation rate at 107, but a log-normal product of gene type times mutation rate of about 1012. So if average mutation rate were 107, this could only apply for 1012/107 = 105 genes. A single gene (100) could mutate as slow as 1012/100 = 1012, or a billion bits of random DNA could mutate as fast as 1012/109 = 103. Actual distribution seems to correlate this. H4 mutates at 1012, but is one of the few genes conserved this much. Modern species such as humans have about 105 genes, but with most of them shared throughout an order. Mammal orders evolve over 107 generations (50 myrs at a generation per five years). Average genes within the order could drift apart at this rate (107) without disrupting the homology of the order. But a smaller number of genes could not alter faster than 108 or 109, without disrupting the homology of the entire class (mammals) or phyla (vertebrae). Alternatively, virus, junk or non-coded DNA can alter almost as fast as it likes without disrupting basic homologies. Only once all places in the gene "spectrum" have been already filled, will we start to get particularly viscous and fast mutating genes, trying to wedge into existence at any place at all.
Again, this log-normal distribution of mutation rates roughly correlates the data, and this author thinks better than a normal distribution. But these assertions are always controversial.
This then is the challenge.
In these chapters we have outlined various controversies surrounding the Theory of Evolution, before proceeding to the main topic, the evolution of human behavior. As we saw, there are now several interesting 'verbal models' of why evolution would occur in a manner better explaining the complexities we know that human behavior entails. But all these verbal models lack a solid mathematical foundation, and so tend to be rejected.
What we have tried to show in this chapter is that the equations, which are a bar to more complex verbal models of evolution, themselves only work for small-scale evolution. We characterize this as evolution at low angles of q , which can be a small number of generations, but not the huge generations in which the basic gene families of modern life evolved. How these genes evolved must be calculated using complex numbers, to account for the vastly different time scales over which genes evolve, when compared to the short life of an individual or lineage. These calculations have not been done. But then again, neither have other anomalies of evolution such as the fall of fitness for sex, or the stepped nature of the fossil record been successfully explained mathematically. Here we only propose a model, not yet developed, to better calculate these types of effects. Plus we propose some tests of how the model would correlate the data, such as be a log-normal distribution of gene mutation rates.
From these few ideas then, can we infer a whole new model of how large-scale change occurs, which can ultimately account for the most complex change: the emergence of intelligent life on Earth?
|
Return to the Theory of Options |
|
|
Previous 2.3 Phylogenic Evolution |
|