Welcome to Mathematics Dictionary
Figure 426 : Petals of R = sin(p*A)

    Petals of R = sin(p*A)


  • Q01 | - Diagram : Petals of R = sin(p*A/q)
  • Q02 | - Prove that the graph of R = sin(p*A/2) has 2*p petals if p is odd
  • Q03 | - Prove that the graph of R = cos(p*A/2) has 2*p petals if p is odd
  • Q04 | - Twin patterns : R = 1 + 1*sin(p*A/2) and R = 1 + 1*cos(p*A/2)
  • Q05 | - Directions of petal of floarl functions
  • Q06 | - References

    Q01. Diagram : graph of R = sin(p*A)
    Graph of R = sin(p*A)
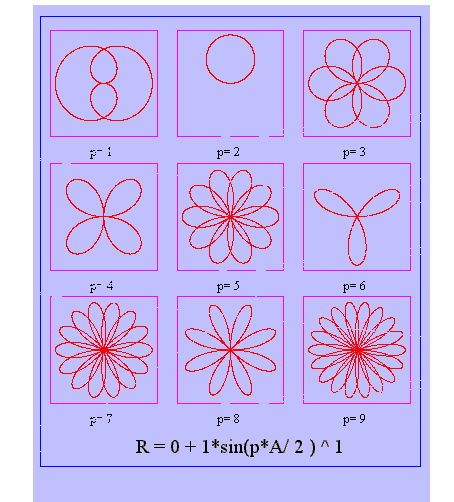
    Graph of R = cos(p*A)

    Go to Begin

    Q02. Prove that the graph of R = sin(p*A/2) has 2*p petals if p is odd

    Graphic solution
    • As shown in Figure 425, the proof is completed
    Numerical proof : Find direction of petals of R = sin(3*A)
    • Number 3*A/2 ... Angle A .. Value R .. Plot angle .. (Direction of Petal)
    • --------------------------------------------------------------------------
    • 1 .... 090 ..... 060 ...... +1 ....... 060 ......... 60
    • 2 .... 270 ..... 180 ...... -1 ....... 000 ......... 180 + 180 - 360 = 0
    • 3 .... 450 ..... 300 ...... +1 ....... 300 ......... 300
    • 4 .... 630 ..... 420 ...... -1 ....... 240 ......... 420 + 180 - 360 = 240
    • 5 .... 810 ..... 540 ...... +1 ....... 180 ......... 540 - 360 = 180
    • 6 .... 990 ..... 660 ...... -1 ....... 120 ......... 660 + 180 - 720 = 120
    • 7 ....1170 ..... 780 ...... +1 ....... 180 ......... 780 -720 = 60
    • Since petal number 1 and petal number 7
      • The petal direction = 60 degrees with petal length = 1
      • Hence it has 6 petals
      • The cycle domain is (780 - 60) = 4*pi
      • Angle A = 0 to 720 degrees
    • Similary we can prove
      • sin(5*A/2) has 10 petals with A = 0 to 4*pi
      • sin(7*A/2) has 14 petals with A = 0 to 4*pi
      • etc.
    Example : Find number of petals of R = sin(4.5*A) with A = 0, 4*pi
    • Since 4.5 = 9/2
    • R = sin(4.5*A) = sin(9*A/2)
    • Hence the number of petals = 2*9 = 18 petals (See diagram)

    Go to Begin

    Q03. Prove that the graph of R = cos(p*A/2) has 2*p petals if p is odd

    Graphic solution
    • As shown in Figure 425, the proof is completed
    Numerical proof : Find direction of petals of R = sin(3*A)
    • Number 3*A/2 ... Angle A .. Value R .. Plot angle .. (Direction of Petal)
    • --------------------------------------------------------------------------
    • 1 .... 000 ..... 000 ...... +1 ....... 000 ......... 0
    • 2 .... 180 ..... 120 ...... -1 ....... 300 ......... 120 + 180 = 300
    • 3 .... 360 ..... 240 ...... +1 ....... 240 ......... 240
    • 4 .... 540 ..... 360 ...... -1 ....... 180 ......... 360 + 180 - 360 = 180
    • 5 .... 720 ..... 480 ...... +1 ....... 120 ......... 480 - 360 = 120
    • 6 .... 900 ..... 600 ...... -1 ....... 060 ......... 600 + 180 - 720 = 60
    • 7 ....1080 ..... 720 ...... +1 ....... 000 ......... 720 -720 = 0
    • Since petal number 1 and petal number 7
      • The petal direction = 0 degrees with petal length = 1
      • Hence it has 6 petals
      • The cycle domain is (720 - 000) = 4*pi
      • Angle A = 0 to 720 degrees
    • Similary we can prove
      • cos(5*A/2) has 10 petals with A = 0 to 4*pi
      • cos(7*A/2) has 14 petals with A = 0 to 4*pi
      • etc.

    Go to Begin

    Q04. Twin patterns : R = 1 + 1*sin(p*A/2) and R = 1 + 1*cos(p*A/2)

    Graphic solution     Compare R = 1 + 1*sin(3*A/2) and R = 1 + 1*cos(3*A/2)
    • The diagrams are no difference : The directions of petals are same
    • But the direction are different if compare the direction
      • ...................... sin .... cos
      • 1st petal direction : 060 .... 000
      • 2nd petal direction : 000 .... 300
      • 3rd petal direction : 300 .... 240
      • 4th petal direction : 240 .... 180
      • 5th petal direction : 180 .... 120
      • 6th petal direction : 120 .... 060

    Go to Begin

    Q05. Directions of petals of floral functions

    1. R = sin(2*A) and R = cos(2*A) : 45 degree phase difference if A = 0, 2*pi 
      1. R = cos(2*A) :  0,  90, 180 and 270 degrees
  2. R = sin(2*A) : 45, 135, 225 and 315 degrees
    2. R = sin(3*A/2) and R = cos(3*A/2) : 0 degree phase difference if A = 0, 4*pi 
      1. R = cos(2*A) :  0,  45, 135, 180, 225, 370, and 315 degrees
  2. R = sin(2*A) :  0,  45, 135, 180, 225, 370, and 315 degrees
    Conclusion 
      Since from the graph we can not tell the function is sine or cosine
  Hence we define R = sin(3*A/2) and R = cos(3*A/2) as twin patterns

    Go to Begin

    Q06. References

    Book
    • Chapter 2 : Graphs of R = sin(n*A)
    • Pictorial Mathematics : Patterns by Dr. Shih
    • P13 - P32
    Computer porgram
    • Mathgraph on personal computer by Dr. Shih
    On internet
    Go to Begin
    • Show Room of MD2002 Contact Dr. Shih Math Examples Room
    Copyright © Dr. K. G. Shih. Nova Scotia, Canada.
    Hosted by www.Geocities.ws

    1