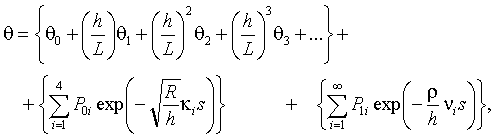
Некоторые вопросы механики сплошной среды
и
математические проблемы теории тонкостенных конструкций
И.И. Ворович, Л.П. Лебедев
Ростовский государственный университет
1. Некоторые общие вопросы механики сплошной среды
В последнее время приходится всё чаще слышать, что уже сейчас компьютеры "умеют решать все задачи механики", а потому традиционная механика постепенно умирает. Это - мнение мальчика, только что научившегося складывать буквы в слова, а потому считающего, что он знает все, что написано в книгах. Применение мощных компьютеров изменяет кардинально наши возможности при решении конкретных задач, часть традиционных задач переходит из сферы теоретических исследований в область практических расчетов. Однако при этом в механике возникает еще более широкая область теоретических исследований, где работа будет производиться не только с помощью традиционной ручки, но и с использованием тех же самых компьютеров. Главным же инструментом исследований все равно останется голова. Как надеются авторы, эта ситуация сохранится в течение весьма долгого времени, по крайней мере, до тех пор, пока будут существовать люди, движимые удивлением явлениями природы, а не только потребительскими проблемами.
Механика, в частности механика сплошной среды, содержит не простой набор фактов и умений расчета сложных конструкций, но также совокупность идей о процессах, происходящих в природных и рукотворных объектах. Наши знания, полученные в результате экспериментальных, расчетных и теоретических работ, постоянно изменяются, трансформируясь в математические модели. Разрабатывая методы расчетов, мы приходим к более глубокому пониманию происходящих явлений. Часто это понимание называют интуитивным, поскольку оно не всегда формализуемо. Интуитивное понимание присуще настоящему исследователю, оно доставляет ему поистине эстетическое наслаждение, оно же является необходимым седьмым чувством для настоящего инженера-практика, проектирующего новые конструкции или процессы. Рутинные вычислительные обязанности, безусловно, будут передаваться компьютерам во все больших объемах. Но для исследователя всегда останется работа по осмыслению результатов, развитию новых общих представлений и теоретических положений, без которых работа компьютеров не может быть полезной.
Значительная часть наших знаний всегда остается неформализованной. Исторически известны примеры, когда, используя весьма скромный по нынешним понятиям набор формул, инженеры проводили успешные расчеты конструкций, требующие сейчас применения суперкомпьютеров. Компьютеры не производят основополагающие идеи. Будучи конечными автоматами, компьютеры имеют преимущество перед человеком, производя гигантское число простейших операций. В то же время компьютер не может выйти за рамки навязанной ему логики, впрочем, как и значительная часть людей. Компьютерные расчеты всегда остаются приближенными, поскольку компьютер производит все действия с числами с ограниченным числом знаков. В то же время сейчас существуют задачи, которые принципиально невозможно решить без применения аналитической части расчета. И хотя многие аналитические действия также станут частью общих компьютерных расчетных и обслуживающих программ, "идеологическая" составляющая теории в течение долгого времени будет привилегией человека.
Компьютерные программы для сложных расчетов, разрабатываемые большими коллективами либо самими же компьютерами, сами становятся предметом для теоретического изучения. Для практического инженера такие программы являются черным ящиком с неизвестными свойствами. Исследователи, занимающиеся научными расчетами, приходят постепенно к мысли, что подобные программы не позволяют им проводить вычисления с той степенью полноты, в которой они нуждаются. Поэтому чуть ли не каждый исследователь составляет свою особую программу для индивидуальных нужд, такую, где он может контролировать события.
Далее, наличие прекрасно представленных результатов расчета есть не более чем фотоснимок реальности. Качественное понимание природы исследуемого объекта или процесса приходит лишь после его теоретического анализа, базирующегося на знании основных теоретических принципов, знании границ применимости используемых моделей процессов и вычислительных методов, которые часто бывают слабо формализованы. Уже стал аксиомой факт, что невежественный человек не может успешно использовать сложное компьютерное математическое обеспечение. Пока что не созданы компьютерные программы для сложных расчетов, работающие по принципу "нажми кнопку и увидишь". И когда они будут созданы, всегда останутся проблемы, не попадающие под общую схему, а, значит, всегда будут люди, занимающиеся теорией для того, чтобы остальные могли бы получать результат, просто нажимая кнопку.
Следует не упускать из виду, что наличие новых вычислительных возможностей неизбежно приводит к новому взгляду на то, что является хорошей моделью в механике и даже, возможно, к частичному пересмотру основ механики сплошной среды. Ограниченные вычислительные возможности прошлого приводили к требованию, чтобы основные модели механики были не слишком громоздкими, что излишне в настоящее время. Важно лишь, чтобы наши модели имели "хорошую математическую природу", что означает, что соответствующие задачи, поставленные на их основе, были бы разрешимыми, а получаемые численно решения обладали гарантированной степенью точности.
Появление мощных компьютеров и компьютерных программ, с помощью которых численно решают многомерные задачи математической физики, приводит к смещению приоритетов проблематики прикладных наук, таких как механика сплошной среды. Решение значительной части традиционных задач механики действительно становится рутинной работой. Появление новых материалов, необходимость решения реальных задач, постановка которых не всегда является классической, выводят на первое место в теории проблему математического моделирования реальных объектов и процессов, исследование моделей и методов решения соответствующих задач. Сюда включается экспериментально-теоретическое изучение адекватности модели реальному объекту и качественное исследование свойств модели. Нам кажется, что существенная часть работы в этом направлении еще долгое время будет принадлежать человеку.
Обратимся, однако, к вопросам теории относительно близкого будущего. Объекты механики сплошной среды, в основном, описываются краевыми либо начально-краевыми задачами для систем уравнений в частных производных. Начальным этапом математического исследования любой модели механики сплошной среды является проблема постановки и разрешимости соответствующих краевых задач. Существование решения в общих условиях не говорит еще о том, что данная модель адекватно описывает объект, но факт принципиальной разрешимости задачи подтверждает ?доброкачественность? ее природы. Дальнейшее исследование должно содержать качественный анализ решений, их сравнение с экспериментальными данными, а также анализ применимости численных методов к решению задач. Отметим, что существует тесная корреляция между проблемой разрешимости краевых задач и возможностью их численного решения. Дальнейшим этапом является изучение качественной картины поведения решений, наличия особенностей решения, исследование критических ситуаций, сравнение с известными экспериментальными данными о самом исследуемом объекте.
Характер соответствия полученного численного результата реальному поведению конструкции или процесса, будучи изначально приближенным, может существенно расходиться с реальностью. Теоретические исследования числовых методов помогают выявить границы возможностей программы, ее надежность с точки зрения конечного результата. Старое высказывание гласит, что нет ничего практичнее хорошей теории.
Попытаемся описать направления, в которых, вероятнее всего, будет развиваться механика недалекого будущего.
2. Некоторые проблемы механики сплошной среды
Комплексный характер проблем реальной жизни вызывает появление математических моделей природных объектов и процессов, сложность и громоздкость которых будет нарастать по мере повышения возможностей вычислительных машин. Механические задачи будут интегрироваться в описание более сложных природных объектов, где необходимо учитывать биологические и др. природные факторы. Наиболее интересные возможности такой интеграции лежат на пути применения методов теории управления объектами и процессами с одновременной идентификацией их изменяющегося состояния. При этом обратные задачи механики сплошной среды будут приобретать все более важную роль. Появление новых постановок задач будет также связано с появлением смешанных способов контроля за системой с передачей компьютеризованной системе данных о системе в реальном времени. К таким задачам можно отнести проблему определения напряжений в телах с предварительно напряженным состоянием.
В отдаленном будущем классические модели механики сплошной среды продолжат свое существование в расчетной области, как первое приближение, с которым можно сравнивать результаты, полученные для более сложных моделей. Кроме того, они будут тестовыми задачами для проверки работоспособности новых вычислительных методов, неизбежно появляющихся для новых задач.
Частными, но важными открытыми математическими проблемами механики сплошной среды являются:
теоремы разрешимости для задач нелинейной теории упругости и остальных моделей механики твердого тела;
способы нахождения изолированных решений в нелинейной упругости;
в гидромеханике теория пограничного слоя получила свое развитие. В механике твердого тела пограничный к поверхности слой также находится в особом состоянии, а потому должен описываться уравнениями, отличающимися от стандартных моделей. На этом пути следует ожидать нового развития асимптотической теории;
имеются задачи, где для получения точного результата необходимо проделать бесконечное число вычислений, ограниченное число шагов приближений может дать достоверный результат лишь в комбинации с аналитическим исследованием. Например, это относится к проблеме устойчивости по Ляпунову многих типов движений. Здесь также возникает необходимость в комбинации асимптотических методов с численными.
Идеология механики сплошной среды, будучи первым приближением для многих проблем реального мира, должна быть дополнена и развита моделями, отражающими атомную структуру вещества. Это необходимое расширение моделей при исследовании вопросов прочности и, в том числе, усталостной прочности. Методы статистической физики должны приобрести существенную роль в развитии механических теорий, поскольку именно они лежат в основе процессов разрушения и прочности. Они будут комбинироваться с существующими методами расчета конструкций и все больше вторгаться в классические области механики сплошной среды.
Естественно, что список открытых проблем и направлений не претендует на какую-либо полноту и охватывает лишь малую часть актуальных проблем механики, где требуется существенное развитие математических методов.
Перейдем теперь к более узкой и специализированной области: к математическим проблемам теории тонкостенных конструкций.
3. Математические проблемы теории тонкостенных конструкций
Строго говоря, все теоретические проблемы теории тонкостенных конструкций относятся к разряду математических, включая многие результаты, полученные численно. Однако сейчас мы рассмотрим те вопросы теории, которые относятся к качественной теории уравнений в частных производных и тесно связаны с механикой деформирования реальных тонкостенных объектов. Термин "тонкостенные конструкции" мы используем для механических объектов один из "размеров" которых существенно меньше остальных. Таким образом, пластины, оболочки, тонкостенные брусья и их комбинации относятся к рассматриваемому классу. Математические вопросы теории тонкостенных конструкций возникают на всех этапах ее развития и применения. Их можно грубо разделить на три класса:
1. проблема точности уравнений, то есть в данном случае это проблема вывода уравнений на основе "точной" трехмерной теории и математических оценок характера приближения;
2. постановка краевых задач теории, их обоснование и качественный анализ поведения их решений;
3. анализ численных методов решения соответствующих краевых задач.
Эти три класса проблем не являются независимыми. Результаты, полученные в одном них, могут применяться для исследования других аспектов теории. Для успешного математического исследования этих задач, как правило, требуется ясное понимание механической природы поведения тонкостенных конструкций под нагрузкой, а не простое применение теорем абстрактной математики.
Обсудим каждую из основных проблем, оставляя детали на дальнейшее. Первое, это проблема адекватности применяемых моделей рассматриваемым объектам. В теории пластин и оболочек уравнения обычно выводятся путем упрощения трехмерных уравнений, которые рассматриваются как относительно точные. Упрощения базируются на кинематических представлениях относительно характера возможных деформаций и ограничениях на распределение напряжений по толщине оболочки. Предположения о характере напряженно-деформированного состояния оболочек базируются на экспериментальных данных и приводят к уравнениям с двумя пространственными независимыми координатами. К математическим здесь относится проблема обоснования перехода от трехмерных задач к двумерным задачам теории пластин и оболочек. С момента написания уравнения теории пластин и оболочек начинают жить независимой жизнью, однако остается вопрос о соотношении между решениями краевых задач теории оболочек и решениями для их трехмерных аналогов. Результаты в этой области имеют асимптотический характер по отношению к малым параметрам, характеризующим тонкостенность оболочек и пластин, а также локально по отношению толщины оболочки к радиусу кривизны граничного контура.
Внутри самой теории оболочек возникает другой круг проблем, связанный с характером уравнений, постановкой краевых задач, поведением решений. Здесь типичными математическими проблемами являются проблема корректности постановки краевых задач (и самой их формулировки, естественно). Для линейной теории - это доказательство теорем существования и единственности в определенных классах решений, исследование характера зависимости решения от внешних факторов и параметров объектов. Для нелинейных задач теории пластин и оболочек, естественно, теорема единственности уже может не выполняться. Здесь возникают другие важные проблемы теории, в частности, проблема устойчивости пластин и оболочек, которая весьма далека от своего полного решения. Качественное поведение оболочки при росте нагрузки и проблема численного нахождения закритических решений -- друга⫻ важная проблема математической теории оболочек.
Отметим, что для практики важное значение имеют задачи о линейных и нелинейных колебаниях оболочек. Это задачи, описывающие явление флаттера в тонкостенных конструкциях, задача о шумовой изоляции. Эти и другие задачи важны практически, но не меньшее значение они имеют и для теории. Для задач о колебаниях особую роль играет вопрос адекватности двумерной модели оболочек и пластин реальным объектам.
Практическая важность третьего круга математических проблем теории оболочек, а именно, вопросов обоснования численных методов расчета конкретных задач, оценок характера сходимости приближений к точному решению, не подлежит сомнению. Достаточно упомянуть о многочисленных вариантах метода конечных элементов и граничных элементов, широко применяемых в практике расчета, но до сих пор имеющих ряд открытых вопросов в теории и практике расчета жизненно важных объектов.
Попытаемся описать состояние дел в математической теории тонкостенных конструкций.
Можно сказать, что начала теории тонкостенных конструкций были заложены Бернулли, который предложил простую, но эффективную схему деформации упругого бруса при изгибе. По этой модели нормаль к нейтральной оси бруса остается прямолинейной и нормальной к деформированной оси, а напряжения в поперечном сечении распределены по линейному закону, так что сопротивление изгибу бруса определяется лишь напряжениями растяжения-сжатия волокон бруса, параллельных нейтральной оси. Основные положения этой схемы были перенесены в теорию пластин и оболочек, и получили название теории оболочек Кирхгофа-Лява. В дальнейшем получили широкое распространение и другие схемы деформирования, например, теории оболочек и пластин Тимошенко и Миндлина-Рейсснера.
Мы не будем здесь обсуждать все варианты различных теорий и не будем составлять списки основополагающих работ в рассматриваемой области, это можно найти в многочисленных обзорах по теории оболочек. Оставляя в стороне исторические вопросы теории, мы рассмотрим лишь некоторые математические аспекты теории пластин и оболочек, их современное состояние и сформулируем некоторые нерешенные здесь проблемы.
Взаимосвязь вопросов математической теории пластин и оболочек с вопросами чистой математики вполне очевидна. Например, в теории Кирхгофа-Лява упругая оболочка представляет собой поверхность, наделенную особыми упругими свойствами по отношению к возможным деформациям под действием нагрузки. Описание кинематики деформации оболочки основано на геометрическом описании срединной поверхности оболочки и, таким образом, связано с вопросами деформации поверхностей, в частности, с классической со времен Гаусса проблемой изгибания поверхностей. Задачи нелинейной теории оболочек, в частности, проблема устойчивости оболочек, при математическом рассмотрении требуют привлечения весьма сложных разделов современной математики, таких как нелинейный функциональный анализ, теория ветвления решений операторных уравнений, асимптотическая теория уравнений с малым параметром при старших производных. Для решения многих вопросов теории современное состояние соответствующих вопросов общей теории является недостаточным и настоятельно требует развития.
3а. Точность уравнений теории пластин и оболочек.
Итак, начнем с рассмотрения первого круга проблем теории оболочек о соотношении между трехмерными задачами теории упругости и двумерными задачами теории оболочек и пластин. Этот вопрос довольно подробно изучался в рамках линейной теории пластин и оболочек теории Кирхгофа-Лява. Результаты здесь носят асимптотический характер. Начало исследований в этом направлении заложено в работе Фридрихса и Дресслера [67]. Существенный вклад в проблему обоснования применимости гипотез Кирхгофа-Лява внесли работы Гольденвейзера и его учеников (см. [31]). Асимптотическая природа характера приближений решений в данной теории была подробно исследована в ростовской школе механиков [1-6, 8, 12, 19-23 и др.] в 1960-1970-х годах. В последнее время западными исследователями был опубликован ряд результатов, повторяющих и развивающих эти исследования. Приведем некоторые результаты этих асимптотических исследований.
Для тонкой однородной изотропной оболочки, рассматриваемой как трехмерное упругое тело, любая компонента тензоров напряжений и деформаций q в окрестности точки границы оболочки может быть асимптотически представлена в виде суммы трех типов слагаемых
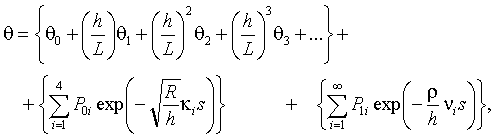
где
-
толщина оболочки, 
-
характерный размер срединной поверхности оболочки,
-
характерный радиус кривизны оболочки в окрестности точки,
радиус
кривизны контура срединной поверхности оболочки и
-
расстояние вдоль нормали от граничной точки срединной поверхности. Положительные
характеристические показатели 
являются
решениями некоторых уравнений, зависящих от параметров оболочки и типа краевых
условий. Степенной асимптотический ряд, стоящий в первых фигурных скобках,
характеризует так называемое проникающее относительно медленно меняющееся
решение. Эта часть разложения присутствует в решении для всех точек оболочки.
Член 
совпадает
с решением, получаемым по теории оболочек Кирхгофа-Лява. Члены, стоящие во
вторых и третьих фигурных скобках относятся к погранслойным составляющим
решения. Это быстро убывающие по мере отдаления от границы члены, практически
исчезающие внутри области. Четыре слагаемых первой серии погранслойных
составляющих решения еще могут быть получены на основе оболочечной теории типа
Кирхгофа-Лява, в то время как члены второй серии погранслойных составляющих
возникают лишь при решении соответствующей трехмерной задачи. Составляющие
решений погранслойного типа могут приводить к существенной концентрации
напряжений вблизи границы оболочек, которая не выявляется при решении конкретных
задач в рамках теории Кирхгофа-Лява.
Помимо такого локального анализа
точности теории оболочек Кирхгофа-Лява были проведены обоснования применимости
данных уравнений на базе интегральных энергетических оценок. Было показано, что
в интегральном смысле уравнения данного типа асимптотически (по отношению к
малому параметру 
)
приближают решение соответствующих трехмерных задач теории упругости. Происходит
это, поскольку в представлении энергии погранслойные составляющие вносят
относительно малый вклад при малых .
Здесь следует упомянуть работы [13,14]. Этому направлению в обосновании теории
оболочек посвящен большой цикл работ французской школы [62,
63]. В последних работах
исследовались несколько теорий пластин и оболочек с точки зрения их
асимптотической точности. Интересные результаты и список работ в данной области
имеется в работе [69].
Для большинства других прикладных теорий пластин и оболочек проблема локального асимптотического исследования погрешности теории в общем виде остается открытой. Также как остаются открытыми и многие вопросы, связанные с погрешностью теории слоистых оболочек, оболочек, выполненных из композитных материалов, а также неупругих оболочек. Одной из открытых проблем является математическое исследование пределов применимости теории оболочек в вопросах колебаний трехмерных конструкций. Для нелинейных теорий оболочек асимптотические результаты относительно их погрешности мало разработаны, однако имеются (см. [64, 61]).
3b. Внутренние математические проблемы теории оболочек
Однажды возникнув на основе некоторых физических соображений как набор некоторых соотношений, уравнений и постановок задач, любая математическая теория начинает жить своей собственной жизнью. Теория пластин и оболочек не является исключением из правила. Основой для вывода соотношений теории пластин и оболочек служат соответствующие части теории механики деформирования трехмерных тел. При математическом исследовании задач мы можем использовать результаты, получаемые в трехмерной теории, как наводящие соображения, однако сами математические результаты в рамках теории оболочек обязаны выводиться лишь с учетом самих соотношений развиваемой теории, например, без использования предположений о малости тех или иных величин, которые были заложены при выводе теории. Естественно, что первые шаги в исследовании математических вопросов теории пластин и оболочек были проделаны в рамках линейной теории упругих оболочек. Несмотря на кажущуюся простоту этих проблем с точки зрения современного аппарата теории уравнений в частных производных даже в этой части теории остались неисследованные вопросы.
Первоначальные способы вывода уравнений упругих оболочек практически повторяли схему вывода уравнений теории упругости, т.е. уравнения равновесия выводились на основе геометрико-силовой картины равновесия элемента оболочки, затем выводились выражения для элементов деформационных тензоров и выводились конституционные соотношения. Другой путь вывода уравнений равновесия упругих оболочек базируется на применении принципа возможных перемещений, сформулированного для трехмерного тела. Кинематические соотношения выводятся отдельно на основе допущений теории и подставляются в трехмерные соотношения общей теории. Из данного интегро-дифференциального уравнения затем выводятся дифференциальные уравнения равновесия (или динамики , с применением принципа Даламбера), а также естественные краевые условия, которые описывают действие внешних сил на границе оболочки. Получаемый на этом пути принцип возможных перемещений для оболочки может непосредственно служить (и служит) для обобщенной постановки соответствующих краевых задач, в рамках которой получаются так называемые слабые (или энергетические) решения задачи. В последнее время интерес к данной постановке задач существенно возрос, поскольку повсеместно используемый для расчетов метод конечного элемента непосредственно дает приближение именно для этого типа решений, используя для своей формулировки, большей частью, именно это уравнение принципа возможных перемещений.
В рамках теории Кирхгофа-Лява соответствующее уравнение принципа возможных перемещений принимает вид
,
(2.1)
где
-
компоненты тензора изменения кривизн срединной поверхности
оболочки,
-
компоненты тензора продольных деформаций срединной поверхности оболочки,
-
компоненты внешних сил, отнесенные к срединной поверхности оболочки и части ее
края 
соответственно,
-
компоненты вектора перемещений срединной поверхности оболочки,
указывает
на то, что в соответствующие компоненты тензоров подставлены компоненты вектора
возможных перемещений 
.
В данном случае тензор напряжений разделяется на две составляющих, тензор
продольных напряжений, компоненты которого
и
тензор моментов с компонентами 
.
Они связаны с деформационными составляющими посредством соотношений обобщенного
закона Гука
(3.2)
(3.3)
Для постановки задачи равновесия
оболочки к вариационному уравнению необходимо присоединить граничные условия.
Формулируя для оболочки краевую задачу равновесия в перемещениях, мы должны
добавить четыре краевых условия в каждой точке границы
области
.
Это могут быть условия жесткого закрепления границы (в этих точках границы
соответствующие компоненты вектора возможных перемещений
должны
равняться нулю, как и соответствующие компоненты вектора
),
условия этого типа будем называть геометрическими. На границе могут быть также
заданы силовые условия, которые следуют из уравнения (3.1) автоматически и при
обобщенной постановке не требуют специального задания. Возможны и смешанные
варианты задания краевых условий, так же как и условия упругого опирания или
условия сопряжения с другими телами.
Математическое обоснование механической модели начинается с выяснения вопросов единственности решения краевых задач в определенных классах функций. Доказательство единственности гладкого решения в линейной задаче равновесия состоит в демонстрации факта, что при однородных краевых геометрических условиях для вектора перемещений уравнение
(3.4)
имеет лишь нулевое решение
.
Левая часть уравнения (3.4) есть выражение удвоенной потенциальной упругой
энергии оболочки, а потому каждое решение уравнения (2.4) можно трактовать как
перемещение оболочки "как жесткого целого". Трудность в доказательстве теорем
единственности для некоторых вариантов линейной теории оболочек здесь возникает
из-за того, что часто эти "жесткие перемещения" отличаются от реальных жестких
перемещений оболочки как трехмерного тела. Например, это происходит в теории
пологих оболочек. Имеется большое число способов доказательств таких теорем
единственности для случая, когда параметры срединной поверхности оболочки
являются достаточно гладкими функциями. Универсальный способ доказательства
таких теорем единственности был развит в [11].
Здесь при достаточно общих краевых условий в рамках теории пологих оболочек было
получено обоснование неравенств, являющихся аналогами неравенства Корна,
выведенного в рамках задач линейной теории упругости. Полные доказательства и
развитие идей доказательства были опубликованы в [8,
25, 24].
Для других теорий оболочек соответствующие неравенства типа Корна выводились
многими авторами, ссылки на работы которых можно найти в [63].
Следует отметить, что в общем случае теоремы единственности в теориях оболочек
были установлены для случая, когда коэффициенты основных квадратичных форм
срединной поверхности оболочки не имели особых точек. Общие теоремы
единственности при наличии сингулярных точек относятся к открытым проблемам
теории оболочек. В общем виде является открытым и вопрос о минимальных условиях
закрепления оболочек, при которых сохраняется единственность решения. В теории
трехмерного упругого тела достаточно закрепить три точки тела, не лежащие на
одной прямой, чтобы классическое решение задачи равновесия оказалось
единственным. Интересно выяснить, какие изменения (если они имеются вообще)
следует внести в формулировку соответствующей теоремы единственности в различных
теориях оболочек.
Следующим после единственности в обосновании доброкачественности постановки краевых задач является вопрос о существовании их решений. При наличии неравенств типа неравенства Корна, выведенных для функционала энергии оболочки, проблема существования решения в линейных задачах равновесия с мертвыми силами решается почти автоматически на основе существующих методов функционального анализа, которые базируются на теории соболевских пространств. Соответствующие теоремы существования решения краевых задач теории оболочек в рамках теории Кирхгофа-Лява были получены как промежуточный результат в работах [11, 8, 25, 24], где изучались соответствующие нелинейные задачи. Обозрение результатов по существованию решения в рамках других теорий можно найти в [63]. Так же как и для теорем единственности открытым остается вопрос о разрешимости задач для оболочек, срединная поверхность которых имеет точки сингулярности, например конического типа. В точках сингулярности срединной поверхности нарушаются механические гипотезы, заложенные при выводе теории оболочки, поэтому сами уравнения в некоторой окрестности таких точек неверны с механической точки зрения. Однако, как уже говорилось, после того, как они выведены, уравнения начинают жить своей собственной жизнью, и здесь возникает чисто математический интерес к постановке задач такого рода с сингулярностью в коэффициентах. Здесь имеет смысл установить, каковы условия, которые необходимо наложить на внешние силы в окрестности сингулярной точки, для того, чтобы соответствующие задачи оказались разрешимыми. Здесь же возникает проблема асимптотического поведения решения соответствующих краевых задач в окрестности точек сингулярности срединной поверхности.
Одной из важных проблем теории является задача исследования регулярности решений краевых задач теории оболочек в зависимости от гладкости внешних сил и параметров оболочки. В большинстве вариантов теории оболочек соответствующая система уравнений относится к классу эллиптических систем, для которых установлено, что внутри области гладкость решения зависит определенным образом от гладкости внешних сил. Такая же зависимость гладкости решения имеет место в окрестности точек границы, где краевой контур является достаточно гладким. Исследование поведения в окрестности угловых точек границы, а также в окрестности точки смены типа краевых условий практически не проводилось, за исключением задач теории пластин.
Получение качественных результатов для динамические задач линейной теории пластин и оболочек (теорем об однозначной разрешимости) не представляет особой сложности, когда имеется теорема об однозначной разрешимости соответствующих задач статики.
Теорема о спектре вполне непрерывного положительно определенного самосопряженного оператора в гильбертовом пространстве полностью решает вопрос о характере распределения собственных частот в задачах для конечных упругих тел (оболочек и пластин, в частности), для которых установлена теорема разрешимости. Для оболочек бесконечной длины, которые могут рассматриваться как волноводы, проблема колебаний, структура спектра задач на собственные значения практически не исследованы, хотя, вероятно, следует ожидать, что спектральные характеристики бесконечных в одном направлении оболочек должны напоминать спектральные характеристики плоской задачи для полосы.
Следует отметить, что для задач для композитных и слоистых оболочек применяются различные методы, связанные с усреднением по толщине упругих коэффициентов. Для таких задач возникают вопросы о степени аппроксимации решения в рамках самой теории оболочек, а также в рамках трехмерных теорий. Здесь же возникает вопрос о возможности применения усредненных коэффициентов для решения задач о колебаниях оболочек и пластин.
Математические вопросы для задач статики и динамики линейных вязкоупругих пластин оболочек решаются достаточно просто. В частности, доказательство разрешимости динамических задач проводится либо с использованием приближенного метода Бубнова-Галеркина с последующим обоснованием предельного перехода, либо методами теории полугрупп. Для вязкоупругих пластин и оболочек недостаточно полно исследован вопрос о режимах поведения вязкоупругих конструкций при больших временах, устойчивость решений по Ляпунову.
Нелинейные задачи теории пластин и оболочек привлекают пристальное внимание теоретиков и практиков в связи с практически важными вопросами устойчивости оболочек, а также в связи с использованием оболочек с нелинейными физическими характеристиками материалов. Данная область математических исследований развивается весьма интенсивно. Ее потребности оказывают существенное влияние на развитие многих вопросов математического анализа нелинейных краевых задач математической физики. Влиянию задач теории упругости на развитие многих вопросов чистой математики посвящены весьма интересные статьи [56, 54]. Задачи общей нелинейной теории упругости чрезвычайно сложны, более того, в общем виде такие проблемы как проблема существования решения задач статики или динамики является практически открытой. Для трехмерных задач существуют лишь частные результаты по существованию решений некоторых задач и теорий, большей частью опирающиеся на принцип Банаха о сжатых отображениях, и, таким образом, дающие лишь результат для относительно небольших нагрузок, где имеется единственность решения соответствующих задач.
В отличие от общей нелинейной теории, в задачах нелинейной теории пластин и оболочек имеется значительный прогресс. Он обусловлен тем, что тип нелинейности уравнений для многих вариантов теории пластин и оболочек существенно проще типа нелинейности уравнений общих нелинейных уравнений теории упругости и поддается исследованиям методами современного функционального анализа. Гипотезы, заложенные при выводе уравнений теории оболочек из соотношений трехмерной теории упругости, кардинально поменяли тип нелинейности уравнений и позволили, с одной стороны, провести качественные исследования краевых задач, а с другой стороны, существенно упростили вычислительные проблемы для соответствующих задач. Именно поэтому они используются при расчете практических конструкций и будут, видимо, использоваться еще в течение продолжительного периода.
Из множества нелинейных статических теорий оболочек наиболее полно математически исследованы два варианта теории физически линейных упругих пологих оболочек, а именно, уравнения Маргерра-Власова и уравнения оболочек типа Кармана. Наиболее простой вариант теории, пластина Кармана, исследовался многочисленными авторами как у нас в стране, так и за рубежом, и методы его исследования уже вошли в учебники по математической физике [35]. Статья [39] была первой публикацией в данном направлении. Это исследование было развито в работах [41, 38, 40, 43]. Рассмотрим сначала, что получено и какие вопросы остались открытыми в рамках этих теорий оболочек Маргерра-Власова и Кармана.
Первые результаты по качественным вопросам теории краевых задач нелинейной теории равновесия упругих оболочек Маргерра-Власова были изложены в работах [13, 14, 17, 18, 9], полное доказательство этих и других результатов было дано в [11]. Расширению теории на случай более сложных краевых условий посвящена работа [25], а окончательная формулировка имеющихся результатов изложена в монографии [8]. Параллельно работам ростовской школы механиков в данном направлении велась работа в Ленинграде, публиковались также работы зарубежных авторов [58, 57, 59, 66 и др.], которые практически повторяли уже полученные в России результаты.
Если первая математическая проблема в линейной теории равновесия ? это получение результатов по единственности решения, то в нелинейной теории возникает проблема неединственности решения. Впрочем, в нелинейной теории оболочек имеется частная, но важная задача о равновесии оболочки без влияния внешних сил, относящаяся к теоремам единственности. Здесь решается вопрос, является ли тривиальное решение единственным решением данной задачи. А если существует нетривиальное решение данной задачи, то какое из решений является более энергетически "выгодным", т.е. какое из решений является более устойчивым. Это важная частная задача теории устойчивости оболочек, которые в случае существования нетривиального устойчивого решения получили название нежестких [8].
Основной шаг в исследовании свойств нелинейных задач теории оболочек ? доказательство теоремы существования. Сначала было доказано существование обобщенного решения задачи в рамках теории Маргерра-Власова. Уравнение, определяющее обобщенное решение, совпадает по форме с уравнением (3.1), по сравнению с линейной теорией меняется лишь вид выражений тензоров деформаций и их вариаций. Задача здесь сводится к решению операторному уравнению
в энергетическом пространстве, которое является подпространством некоторого соболевского пространства. Доказательство теорем существования здесь можно проводить двумя методами: доказывая принципиальную возможность решения этих задач с помощью приближенных методов, в частности проекционных методов, а также с использованием теории вращения вполне непрерывных векторных полей. Основным элементом доказательства соответствующих результатов в обоих случаях является получение глобальной априорной оценки всех возможных решений. Проведенное математическое доказательство оценки существенно опирается на механический смысл уравнений, понимание, как распределяется энергия деформации в общем случае для различных типов деформации.
Аналогичное доказательство теоремы существования было проведено в теории упругих пологих оболочек типа Кармана. Интересно отметить, что здесь основной момент доказательства, получение априорной оценки решений, также базировался на механических соображениях, но использовал методы дифференциальной геометрии.
Теоремы существования в обоих случаях были доказаны при весьма общих краевых условиях, однако для ряда естественных краевых условий соответствующие результаты не получены и по сей день. Почему это происходит, легко понять, если принять во внимание, что, например, уравнения Маргерра-Власова, с точки зрения общей теории механики сплошной среды являются "плохими": они неинвариантны при смещении оболочки как жесткого целого, т.е. при таком смещении могут возникнуть дополнительные напряжения, которых не наблюдается, если рассматривать оболочку как трехмерный объект. Возможно, поэтому при доказательстве теоремы о разрешимости возникает необходимость "избыточного" закрепления оболочки по краям.
В нелинейной теории краевых задач математической физики значительная часть результатов основана на применении теории монотонных операторов. В теории оболочек получающиеся операторы не являются монотонными. Почти очевидно, что возможно обобщение полученных для оболочечных задач результатов по теоремам разрешимости на случай абстрактных уравнений математической физики, однако это до сих пор не проделано.
Некоторые качественные результаты, касающиеся корректности постановки задач теории оболочек были получены в [26, 32].
Для нелинейной теории непологих упругих оболочек теорема существования была получена лишь при некоторых дополнительных ограничениях [28, 30] на коэффициенты основных квадратичных форм срединной поверхности оболочки. Для теорий физически и геометрически нелинейных оболочек общих теорем существования для двумерных задач неизвестно, так же как неизвестно их и для теорий оболочек Тимошенко и Миндлина-Рейсснера. Одномерные задачи для последних рассматривались несколькими авторами.
В нелинейной теории оболочек существенный интерес вызывают проблемы устойчивости. Задачи на устойчивость решаются, в основном, численно. Однако здесь имеются важные теоретические результаты для частных случаев. Например, в теории пластин Кармана обоснована применимость метода линеаризации Эйлера [9, 8]. Понятие устойчивости оболочек и способы его практического определения всё еще нуждаются в теоретической разработке. Некоторые теоретические положения были получены здесь в работах [9, 8, 46, 45]. Исследование поведения пластин и оболочек после потери устойчивости, основанное на теории ветвления решений операторных уравнений, была проведено в [16, 45, 8], а также в работах других авторов. Следует отметить, что возможности теоретических исследований в этом направлении, в частности, числа решений и характера их распределения в зависимости от нагрузки, далеко не исчерпаны. Очевидно, что в данных задачах могут быть применены вариационные методы исследований, как это было продемонстрировано в фундаментальной монографии [55].
К проблемам математического характера здесь также относится проблема регулярности решения, зависимости гладкости решения от гладкости действующих сил. Данная проблема решена в теории пологих оболочек в [11, 8] относительно гладкости решения внутри области и вблизи гладкой части границы. Значительно слабее данная зависимость исследована в окрестности угловых точек границы срединной поверхности. Авторам неизвестны результаты по гладкости решений в других теориях оболочек, хотя принципиальных трудностей по переносу соответствующих результатов из теории пологих оболочек не ожидается.
Следует отметить слабую исследованность нелинейных задач теории оболочек с препятствиями.
Важную роль в проблеме устойчивости оболочек играют статистические соображения. Некоторые статистические проблемы теории оболочек изучались в [7, 47, 49].
Теоремы существования обобщенных решений в нелинейных задачах динамики упругих оболочек развиты с достаточной степенью полноты для вариантов, основанных на гипотезах Кирхгофа-Лява [15, 57, 42, 24]. В проблеме единственности энергетического решения, поставленной много лет назад, был получен частичный ответ: в [44, 70] для пологой оболочки была получена теорема единственности для того же класса решений, где доказана теорема существования. Однако окончательный результат ожидает своего решения. В работах [60, 47-51] изучалась структура аттрактора решений в задачах нелинейной теории пластин Кармана. Теоремы существования и некоторые другие математические вопросы нелинейной теории вязкоупругих оболочек изучались для различных вариантов вязкоупругости в [24, 34, 33, 68]. Следует отметить слабую исследованность этих вопросов для оболочек в рамках теории пластичности.
3с. Математические вопросы численного анализа в теории оболочек и пластин
Всякая модель механики сплошной среды начинается с выбора вида тензоров деформаций, напряжений и их связи. Для оболочек и пластин уже этот этап носит существенно приближенный характер. По этой причине мы не можем просто заявить, что решение задач теории оболочек обязано существовать, поскольку это очевидно из механических соображений. Конечно, было бы хорошо уметь решать самые общие задачи в точной трехмерной постановке, но для этого имеются объективные препятствия, связанные со сложностью расчета трехмерных задач, с наличием погранслойных составляющих в их решении. Благодаря удачно выбранным гипотезам теории оболочек, численное "оболочечное решение" может оказаться более точным по сравнению с численным решением соответствующей трехмерной задачи при тех же затратах машинного времени и других ресурсов даже в случае линейных задач. А в нелинейном варианте имеется уже очевидное преимущество за уравнениями оболочек, поскольку для трехмерных задач при средних и больших нагрузках требуется решать весьма большие системы нелинейных уравнений, в то время как в оболочечном варианте, во первых, число уравнений и неизвестных существенно меньше за счет уменьшения размерности, а во вторых, вывод уравнений оболочек произведен так, что уравнения оболочек по своей структуре существенно лучше приспособлены для численного решения, чем уравнения трехмерной теории. Поэтому в нелинейной теории при численном решении выбор между точной постановкой задач и приближенной ?оболочечной? завершается в пользу последней.
Различные модификации численных методов для решения линейных задач по теории пластин и оболочек исследовались огромным числом авторов, доказывалась и сходимость различных методов, и исследовались вопросы скорости их сходимости. Здесь имеется огромное число теоретических работ, связанных с разработкой различных вариантов методов и их обоснований. Обозрение некоторой части работ в этом направлении (достаточно старое, но все еще не устаревшее) можно найти в [66].
Проблеме обоснования различных численных методов в нелинейной теории пластин и оболочек посвящено значительно меньшее число работ. Из всех вариантов численного решения задач в нелинейной теории оболочек и пластин на практике сохранились вариационно-разностные методы [36, 37], проекционные методы и метод конечного элемента, который во многих случаях является одной из модификаций последних. Первыми работами в этой области были [13, 14], посвященные применению метода Бубнова-Галеркина в нелинейной теории пологих оболочек (вариант Власова). Для более общих уравнений упругих пологих оболочек проблема обоснования проекционных методов была исследована топологическими и вариационными методами в [11, 8, 27]. Здесь же для некоторых вариантов используемых методов были получены оценки скорости сходимости приближений. Следует отметить, что разрешимость конечномерных уравнений метода Бубнова-Галеркина в каждом приближении доказывается относительно несложно в тех случаях, когда установлены априорные оценки решений задачи в целом в энергетических классах решений. Отметим, что доказательство разрешимости уравнений метода Бубнова-Галеркина получается и для многих других задач, где разрешимость задач в целом еще не установлена. Такова ситуация для различных вариантов задач статики и динамики нелинейной теории упругости, пространственных уравнений Навье-Стокса (в энергетических классах решений) и многих других. Таким образом, теоретическая возможность нахождения некоего приближения часто оказывается обоснованной. Тот факт, что можно численно найти решение задачи при любых нагрузочных членах, многими практиками трактуется как свидетельство, что сама первоначальная задача всегда разрешима. Однако это не всегда так. Следует иметь в виду, что пока что нет общих методов, позволяющих только на основе численных данных утверждать о сходимости приближенных решений к точному. Этому препятствует конечность разрядной сетки компьютера, более того, имеется некоторый предел достижимой точности численных решений краевых задач, который не может быть превышен принципиально на данном компьютере. Обычный метод практического ?обоснования? сходимости численного метода, когда численное решение проводится с большим числом базисных элементов или точек разбиения области и т.п., затем приближение более высокого порядка сравнивается с предыдущим, а их близость служит критерием сходимости метода, может лишь свидетельствовать о том, что результат для следующего приближения изменится не слишком сильно. Этот практический прием не является обоснованием сходимости численного метода, которая должна исследоваться отдельно. Доказательство теорем разрешимости с использованием проекционных методов обосновывает сходимость этих методов и дает реальную базу для утверждения о близости компьютерных решений к истинным. Это же доказательство указывает характер сходимости приближений.
В заключение отметим, что число математических вопросов, связанное с вычислительными проблемами механики тонкостенных конструкций постоянно возрастает. Это связано как с разработкой теории самих вычислительных процедур, так и со все усложняющимися конституционными соотношениями и самими вариантами теорий пластин и оболочек. Особый интерес здесь вызывают методы, основанные на комбинации численных и классических аналитических методов.
Литература
1. Аксентян О.К., Ворович И.И. Напряженное состояние плиты малой толщины// Прикл. матем. и механика. ? 1963. ? 27, вып. 6. ? С. 1057?1074.
2. Базаренко Н.А., Ворович И.И. Асимптотическое поведение решения задачи теории упругости для полого цилиндра конечной длины при малой толщине// Прикл. матем. и механика. ? 1965. ? 29, вып. 6. ? С. 1035?1052.
3. Базаренко Н.А., Ворович И.И. Асимптотическое поведение решений задачи теории упругости для полого цилиндра конечной длины при малой толщине// Аннот. докл. 5 Всесоюзн. конференции по теории пластин и оболочек. ? М. ? 1965. ? С. 15.
4. Виленская Т.В., Ворович И.И. Асимптотическое поведение решения задач теории упругости для незамкнутой полой сферы при малой толщине// Аннот. докл., 5 Всесоюзная конференция по теории пластин и оболочек. ? М. ? 1965. ? С. 15?16.
5. Виленская Т.В., Ворович И.И. Асимптотическое поведение решений задач теории упругости для сферической оболочки малой толщины// Прикл. матем. и механика. ? 1966. ? 30, вып. 2. ? С. 278?295.
6. Ворович И.И. Некоторые математические проблемы теории пластин и оболочек// 2 Всесоюзный съезд по теор. и прикладной механике, аннот. докладов. ? М. ? 1964. ? С. 56?57.
7. Ворович И.И. Статистический метод в теории устойчивости оболочек// Прикл. матем. и механика. ? 1959. ? 23, вып. 5. ? С. 885?892.
8. Ворович И.И. Математические проблемы нелинейной теории пологих оболочек. ? М.: Наука, Гл. ред. физ.?мат. лит?ры, 1989. ?376 с.
9. Ворович И.И. Некоторые вопросы устойчивости оболочек в большом// ДАН СССР. ? 1958. ? 122, №1. ? С. 37-40.
10. Ворович И.И. Некоторые математические вопросы теории пластин и оболочек// Аннот. докл., 5 Всесоюзная конференция по теории пластин и оболочек. ? М., 1965. ? С. 116?136.
11. Ворович И.И. Некоторые математические вопросы нелинейной теории оболочек. Докторская диссертация. ? Ростов?на?Дону, 1958. ? 366 с.
12. Ворович И.И. Некоторые проблемы концентрации напряжений// Концентрация напряжений. Вып. 2. Доклады на 2?м симпозиуме по концентрации напряжений вблизи отверстий в пластинах и оболочках. ? Киев: Наукова думка, 1968. ? С. 45?53.
13. Ворович И.И. О некоторых прямых методах в нелинейной теории пологих оболочек// ДАН СССР. ? 1955. ?105, №1. ? С. 42?45.
14. Ворович И.И. О некоторых прямых методах в нелинейной теории пологих оболочек// Прикл. матем. и механика. ? 1956. ? 20, вып. 4. ? С. 449?474.
15. Ворович И.И. О некоторых прямых методах в нелинейной теории колебаний пологих оболочек// Изв. АН СССР. Сер. Математика. ? 1957. ? 21, №6. ? С. 747?784.
16. Ворович И.И. О поведении круглой плиты после потери устойчивости// Уч. зап. Ростовского ун?та. ? 1955. ?32, №4. ? С. 55?60.
17. Ворович И.И. О существовании решений в нелинейной теории оболочек// Изв. АН СССР. Сер. Математика. ? 1955. ? 19, №4. ? С. 173?183.
18. Ворович И.И. О существовании решений в нелинейной теории оболочек// ДАН СССР, 1957. ? 117, № 2. ? С. 203?206.
19. Ворович И.И., Аксентян О.К. Об определении концентрации напряжений на основе прикладной теории// Прикл. матем. и механика. ? 1964. ? 28, вып 3. ? С. 589?596.
20. Ворович И.И., Аксентян О.К. Об определении концентрации напряжений на основе прикладной теории// Концентр. напряжений, доклад на симпозиуме по концентр. напряжений около отверстий в пластинах и оболочках. ? Киев. ? 1965. ? 1. ? С. 93?94.
21. Ворович И.И., Базаренко Н.А. Анализ трехмерного напряженного и деформированного состояния круговых цилиндрических оболочек. Построение уточнённых прикладных теорий// Прикл. матем. и механика. ? 1969. ? 33, вып. 3. ? С. 495?510.
22. Ворович И.И., Кадомцев И.Г. Качественное исследование напряженно?деформированного состояния трехслойной плиты// Прикл. матем. и механика. ? 1970. ? 34, вып. 5. ? С. 870?876.
23. Ворович И.И., Кадомцев И.Г., Устинов Ю.А. Некоторые общие свойства трехмерного напряженно?деформированного состояния трехслойной плиты симметричного строения// Всесоюзная конференция по теории оболочек и пластин. Труды 9-й конференции, 27?28, дек. 1973. ? Л.: Судостроение, 1975. ? С. 36?37.
24. Ворович И.И., Лебедев Л.П. О методе Бубнова?Галеркина в нелинейной теории колебаний вязкоупругих оболочек// Прикл. математика и механика. ? 1973. ? 37, вып. 6. ? С. 1117?1124.
25. Ворович И.И., Лебедев Л.П. О существовании решений в нелинейной теории пологих оболочек// Прикладная математика и механика. 1972. ? 36, вып. 4. ? С. 691?704.
26. Ворович И.И., Лебедев Л.П. О корректности задачи статики нелинейной теории упругих пологих оболочек// Прикл. матем. и механика. ? 1998. ? 62, вып. 4. ? С. 678?682.
27. Ворович И.И., Лебедев Л.П. О методе конечных элементов в нелинейной теории оболочек// Rus. Journ. Comput. Mechanics. ? 1993. ? 1, №1. ? С. 1?21.
28. Ворович И.И., Лебедев Л.П., Шлафман Ш.М. О некоторых прямых методах и существовании решения в нелинейной теории упругих непологих оболочек вращения// Прикладная математика и механика. ? 1974. ? 38, вып. 2. ? С. 339?348.
29. Ворович И.И., Малкина О.С. О точности асимптотических разложений решения задачи теории упругости для толстой плиты// Изв. АН СССР. Сер. Механика твердого тела. ? 1967, 5. ? С. 92?102.
30. Ворович И.И., Шлафман Ш.М. О разрешимости нелинейных уравнений для симметрично нагруженного непологого сферического купола// Прикл. матем. и механика. ? 1974. ? 38, вып. 5. ? С. 944?946.
31. Гольденвейзер А.Л. Теория тонких упругих оболочек; М., Наука, 1976. ? 512 с.
32. Лебедев Л.П. К вопросу о разрешимости нелинейных задач статики упругих пологих оболочек// ДАН. ? 1998. ? 363, №.4. ? С. 486?488.
33. Лебедев Л.П. О разрешимости нелинейных задач динамики вязкоупругих оболочек// ДАН. ? 1998. ? 361, №2. ? С. 201?203.
34. Лебедев Л.П. О решении динамической задачи вязкоупругих оболочек// ДАН СССР. ? 1982. ? 267, №1. ? С. 62?64.
35. Лионс Ж.?Л. Некоторые методы решения нелинейных краевых задач; М., Мир, 1972. ? 587 с.
36. Масловская Л.В. О сходимости вариационно?разностных методов для нелинейных краевых задач теории упругих пластин// ЖВМ и МФ. ? 1979. ? 18, №.4. ? С. 122?129.
37. Масловская Л.В., Вербицкий В.В. Сходимость смешанного метода конечного элемента в задачах устойчивости пологих оболочек// Изв. ВУЗов. Сер. Математика. ? 1993. ? №10. ? С. 21?31.
38. Морозов Н.Ф. К вопросу о существовании несимметричного решения в задаче о больших прогибах круглой пластинки. загруженной симметричной нагрузкой// Изв. ВУЗов. Сер. Математика. ? 1961. ? №2. ? С. 126?129.
39. Морозов Н.Ф. К нелинейной теории тонких пластин// ДАН СССР. ? 1957. ? 114, №5. ? С. 968?971.
40. Морозов Н.Ф. К нелинейным задачам теории тонких пластин с р осями симметрии// ДАН БССР. ? 1963. ?7, №6. ? С. 128-133.
41. Морозов Н.Ф. Нелинейные задачи теории тонких анизотропных пластин// Изв. ВУЗов, Математика. ? 1960. ? №6. ? С. 170?173
42. Морозов Н.Ф. О нелинейных колебаниях тонких пластин с учетом инерции вращения// ДАН СССР. ? 1967. ? 176, №3. ? С. 522?525
43. Морозов Н.Ф. Существование гладкого решения задачи о нелинейных колебаниях тонкой пластины// ЖВМ и МФ. ? 1966. ? 6, №4. ? С. 773?776.
44. Седенко В.И. Единственность обобщенного решения начально?краевой задачи в нелинейной теории колебаний пологих оболочек// ДАН СССР. ? 1991. ? 316, №.6. ? С. 1319?1322.
45. Срубщик С.Л. Выпучивание и послекритическое поведение оболочек. ? Ростовский?на?Дону ун?т, 1981. ?95 с.
46. Срубщик С.Л., Юдович В.И. Замечание об устойчивости мембранных решений в нелинейной теории пластин и оболочек// Прикл. математика и механика. ? 1966. ?30, вып. 1. ? С. 116?123.
47. Чуешов И.Д. Существование статистических решений стохастической системы уравнений фон Кармана в ограниченной области// Мат. сборник. Нов. сер. ? 1983. ? 122(164), №3. ? С. 291?312.
48. Чуешов И.Д. Конечная размерность аттрактора для некоторых задач нелинейной теории оболочек// Мат. сборник. Нов. сер. ? 1987. ? 133(175), №4(8) . ? С. 419?428.
49. Чуешов И.Д. О статистических решениях стохастической системы уравнений Кармана// Доклады НАН Украины. Сер. A. ? 1982, №.9. ? С. 26?29.
50. Чуешов И.Д. Сильные решения и аттрактор системы уравнений Кармана// Доклады НАН Украины. Сер. A. ? 1988. ? № 5. ? С. 22?25.
51. Чуешов И.Д. Сильные решения и аттрактор системы уравнений Кармана// Мат. сборник. ? 1991. ? 181, №1. ? С. 25?36.
52. Шойхет Б.А. Об асимптотически точных уравнениях тонких плит сложной структуры// Прикл. матем. и механика. ? 1973. ? 37, вып. 5. ? С. 914?924.
53. Шойхет Б.А. Одно энергетическое тождество в физически нелинейной упругости и оценки погрешности уравнений плит// Прикл. матем. и механика. ? 1976. ? 40, вып. 2. ? С. 317?326.
54. Antman S.S. Nonlinear continuum physics// Mathematics Unlimited ? 2001 and Beyond. ?Springer-Verlag. ? 2001. ? 1237 p.
55. Antman S.S. Nonlinear problems of elasticity. ? Springer-Verlag, New York, 1996. 750 p.
56. Antman S.S. The influence of elasticity on analysis: modern developments// Bulletin of the American Mathematical Society. ? 1983. ? 9, no. 3. ? P. 267?291.
57. Berger M. S., Fife P. C. Von Karman?s equations and the buckling of a thin elastic plate. II: Plate with general edge conditions. Part 2// Comm. Pure Appl. Math. ? 1968. ? 21. ? P. 227?241.
58. Berger M. S. Von Karman?s equations and the buckling of a thin elastic plate. Part 1// Comm. Pure Appl. Math. ? 1967. ? 20, no. 4. ? P. 687?719.
59. Bernadou M., Oden J.T. An existence theorem for a class of nonlinear shallow shell problems// J. Math. Pures et Appl. ? 1981. ? 60. ? P. 285?308.
60. Chueshov I.D. Regularity of solutions and approximate inertial manifolds for von Karman evolution equations// Math. Methods Appl. Sci. ? 1994. ? 17, no.9. ? P. 667?680.
61. Ciarlet P.G., Roquefort, A. Justification of a two?dimensional nonlinear shell model of Koiter's type// Chinese Ann. Math. Ser. B 22. ? 2001. ? 2. ? P. 129?144.
62. Ciarlet P.G., Destuynder P. A justification of the two?dimensional linear plate model// J. M?anique. ? 1979. ? 18. ? P. 315?344.
63. Ciarlet P.G. Mathematical elasticity. Volume 3: Theory of shells. ? North Holland, 2000. 666 p.
64. Ciarlet P.G., Paumier J.C. A justification of the Marguerre von Karman equations for shallow shells// Comptes Rendus de l? Academie des Sciences serie I?Mathematique. ? 1985. ? 301, no.18. ? P. 857?860.
65. Ciarlet P.G. The Finite Element Method for Elliptic Problems. ? North Holland, 1978. 530 p.
66. Cibula J. Von Karman equations iii. Solvability of the von Karman equations with conditions for geometry of the boudary of the domain// Applications of mathematics. ? 1991. ?36, no.5. ? P. 368?379.
67. Friedrichs K.O., Dressler R.F. A boundary layer theory for elastic plates// Comm. Pure and Appl. Math. ? 1961. ? 14. ? P. 1?33.
68. Lebedev L.P., Kalpakides V.K., Foutsitzi G. Solvability of boundary value problems of the dynamics of nonlinear viscoelastic shells// Mathematics and Mechanics of Solids. ? 2001. ?6, no.1. ? P. 65?86.
69. Motygin O.V., Nazarov S.A. Justification of the Kirchhoff hypotheses and error estimation for two?dimensional models of anisotropic and inhomogeneous plates, including laminated plates// IMA Journal of Applied Mathematics. ? 2000, ? No. 64. ? P. 1?28.
70. Sedenko V.I. On the uniqueness theorem for generalized solutions of initial?boundary problems for the Maguerre?Vlasov vibrations of shallow shells with clamped boundary conditions// Appl. Math. Optimization. ? 1999. ? 39, no.3. ? P. 309?326.
Some questions of the continuum mechanics and mathematical problems of the theory of thin-walled structures
I.I. Vorovich, L.P. Lebedev
Rostov State University
The application of increasingly powerful computers has altered the general viewpoint on what constitutes a real research problem in continuum mechanics. Problems that were once considered intractable by scientists are now solved on a routine basis by design engineers. Researchers are therefore returning to their primary roles: the composition and study of new, more accurate, and more reliable models for mechanical objects. This necessitates both a deeper understanding and better description of the physical processes that occur inside the bodies, and the development of new mathematical tools aimed at the study of more complex boundary value problems. This paper presents the state of the art and some mathematical problems arising in the theory of plates and shells. The principal directions taken by the mathematical theory in this area are also discussed. There is an overview of the existing mathematical results in the linear and nonlinear theories of shells and plates, and some open problems of these theories are stated.
Реферат
Некоторые вопросы механики сплошной среды и математические проблемы теории тонкостенных конструкций
И.И. Ворович, Л.П. Лебедев
Ростовский государственный университет
Все более широкое использование мощных компьютеров изменило понимание, что собой представляют настоящие исследования в механике сплошной среды. Задачи, которые ранее были недоступны для решения, сейчас решаются обычными инженерами с помощью стандартных программ. Таким образом, ученые-механики возвращаются к функциям, которые были свойственны начальным этапам развития механики: созданию и изучению новых, более точных и надежных моделей для механических объектов. Это приводит к необходимости более глубокого понимания и более точного описания физических процессов, проходящих внутри тел, а также к развитию новых математических методов для изучения более сложных новых краевых задач механики. Данная статья представляет состояние дел и некоторые математические проблемы, возникающие в теории пластин и оболочек. Здесь же обсуждаются главные направления теоретических исследований в данной области. Приводится обозрение существующих математических результатов в линейной и нелинейной теории пластин и оболочек, а также формулируются некоторые открытые проблемы и нерешенные задачи данной теории.
Сведения об авторах.
И.И. Ворович ? академик РАН
Л.П. Лебедев ? д.ф.м.н., проф. каф теории упругости РГУ, в настоящее время работает в Universidad Nacional, Богота (Колумбия)
e-mail: [email protected]