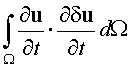 +
òW [cijklqkl
dqij +
+
òW [cijklqkl
dqij +И.И. Ворович, Л.П. Лебедев
Появление компьютерных программ типа ANSYS, с помощью которых численно решают многомерные задачи математической физики, привело к смещению приоритетов проблематики прикладных наук, таких как механика сплошной среды. Решение значительной части задач механики становится рутинной работой, где на первое место выходят проблемы надежности полученных численных результатов, их соответствия численных решений экспериментальным данным. Появление новых материалов, а также необходимость решения реальных задач, постановка которых не всегда является классической, выводят на первое место в теории проблему математического моделирования реальных объектов и процессов и теоретического их исследования. Последнее включает в себя вопросы сходимости применяемых численных методов, в частности, одного из наиболее широко применяемых методов, метода конечных элементов. Роль теоретических исследований приобретает особое значение в связи с тем, что большинство стандартных программ численного решения задач является для пользователя своеобразным «черным ящиком». Характер соответствия полученного численного результата реальному поведению конструкции под нагрузкой или процессу, будучи изначально приближенным, может существенно расходиться с реальностью. Теоретические исследования помогают выявить границы возможностей общих программ, их надежность с точки зрения конечного результата. Старое высказывание гласит, что нет ничего практичнее хорошей теории.
Начальным этапом математического исследования любой модели механики сплошной среды является проблема постановки и разрешимости краевых задач. Существование решения для произвольных внешних нагрузок не является достаточным признаком работоспособности модели, однако факт принципиальной разрешимости задач подтверждает «доброкачественную» природу модели. Дальнейшее исследование должно содержать качественный анализ решений, их сравнение с экспериментальными данными, а также анализ применимости численных методов к решению задач. Существует тесная корреляция между проблемой разрешимости краевых задач и возможностью их численного решения. Рассмотрим некоторые аспекты этой связи на примере задач нелинейной теории вязкоупругих оболочек.
Всякая модель механики сплошной среды начинается с выбора вида геометрических характеристик деформации, используемых тензоров напряжений и их связи. Для вязкоупругих оболочек уже этот этап имеет приближенный характер. По этой причине мы не можем просто заявить, что решение такой задачи обязано существовать, поскольку это очевидно из механических соображений. Конечно, было бы хорошо решать самые общие задачи в точной трехмерной постановке, но для этого имеются объективные препятствия, связанные как с нелинейностью задач, приводящей к тому, что современные компьютеры не могут их обсчитывать в многомерной постановке, так и в элементарном отсутствии данных по экспериментальной «оцифровке» определяющих соотношений более точных моделей. Поэтому выбор между точной постановкой задач и приближенной «оболочечной» завершается в пользу «надежности», т.е. в пользу постановки задач, когда с самого начала применяется гипотезы теории оболочек.
Рассмотрим вариант нелинейной теории оболочек, базирующийся на гипотезах Кирхгофа-Лява. Оболочка является трехмерным телом, однако для ее описания используются характеристики, заданные на срединной поверхности S [1,2]. Пусть S – достаточно гладкая поверхность, отображаемая на связное ограниченное (открытое) множество W с кусочно-гладкой границей ¶W в плоскости R2 и x=(x1, x2) Î W – криволинейные координаты на S. Положение точки на S задается вектором r = r(x1, x2). Обозначим aa = ¶r/¶xa. Предположим, что координатная сетка нигде не вырождается в области W. Будем также придерживаться обычного в тензорной алгебре правила суммирования по повторяющимся верхним и нижним индексам. Введем вектор нормали к S, имеющий вид a3 = a1 ´ a2 / |a1 ´ a2 |, а также вектора взаимного базиса, определенные соотношением aa× ab = dab, где dab - символ Кронекера. Коэффициенты первой и второй квадратичных форм срединной поверхности есть aab = aba = aa × ab , bab = bba = - aa × a3,b , где индексы a или b после запятой означают частные производные по xa, xb. Ковариантные производные компонент произвольного вектора u = ui ai, iÎ{1, 2, 3} даются следующими формулами
ua|b= ua,b - Гkabuk , ua|b =ua,b + Гabkuk, u3|a = u3,a,
Деформация в непологой теории оболочек «среднего» изгиба описывается тензором деформаций срединной поверхности g = gabaaab и тензором изменения кривизн срединной поверхности r = rabaaab с компонентами gab = qab + 1/2 jajb, rab= 1/2 (ja|b + jb|a), где qab = 1/2 (ua|b + ub|a) – bab w – компоненты линеаризованного тензора деформации срединной поверхности, а ja = w,a + balul º w,a + bla ul – углы поворота нормали к срединной поверхности. Для нормальной компоненты u3 вектора перемещений используем обозначения wºu3ºu3.
Напряжения в оболочке характеризуются тензором продольных усилий n = nabaaab и тензором моментов m = mabaaab. Определяющие соотношения вязкоупругой оболочки берутся в форме
nij= nij0(t) + cijklgkl -ò0 T Эijkl(t, t) gkl(t)dt,
mij= mij0(t) + h2/12 cijklrkl - h2/12ò0 T Эijkl(t, t) rkl(t)dt,
которые в тензорной форме принимают вид:
n=n0(t) + nупр + nв , m= m0(t) + mупр + mв.
Здесь n0(t) и m0(t) являются известными тензор-функциями от пространственных переменных, зависимость от которых явно не указывается, и времени t. Члены nупр= С××g, и mупр= h2/12 С××r (точка «×» – знак свертки) описывают «мгновенную упругую реакцию» в элементе оболочки. Формально эти соотношения совпадают с определяющими соотношениями для упругих оболочек. Пусть тензор мгновенно упругих постоянных С=(cijkl) является положительно определенным, т. е. существует такая постоянная m > 0, что для всех симметричных тензоров g выполнено неравенство
cijklgkl gij ³ m gkl gkl .
«Вязкие» свойства оболочки описываются членами nв и mв , содержащими интегралы по времени. Будем предполагать, что ядра релаксации Эijkl(t, t) являются гладкими функциями времени.
Уравнения движения оболочки записываются с помощью принципа виртуальных перемещений:
òW{nab dgab +mab drab}dW =òW{F i dui - rh ¶2ui/¶t2 dui}dW, (1)
где dW = Jdx1dx2, J2= a11a22 – a122, а вариации даются формулами
dgab=0.5(dua|b+ dub|a) -bab dw + 0.5 (dja jb+ ja djb),
dja= dw,a + bal dul=dw,a + bla dul, drab=0.5 (dja|b+djb|a) .
Уравнения в дифференциальной форме выводятся с помощью стандартной техники вариационного исчисления. Уравнение (1) кладется в основу определения обобщенного решения задачи. Для этого его следует проинтегрировать по времени в пределах от 0 до Т, после чего произвести переброску производных по времени по частям в динамическом члене, считая, что du(x, T) = 0. Имеем:
ò0 T òW{nab dgab +mab drab}dW dt =
=ò0 T òW{F i dui+rh ¶ui/¶t ¶dui/¶t}dW dt +òW rh u1i duidW |t=0 , (2)
где u1i=¶ui/¶t|t=0 – заданное начальное значение.
Будем рассматривать непологие оболочки с жестко закрепленным краем:
u|¶W = 0, ¶u3/¶n|¶W = 0. (3)
Для достаточно гладких вектор-функций u(x), удовлетворяющих краевому условию (3), введем скалярное произведение
(u, du)H = òW {hcijkl qkl dq ij +h3/12 cijklrkl drij }dW.
Замыкание данного множества вектор-функций в соответствующей норме || u ||H = (u, u)H1/2 есть энергетическое пространство, обозначаемое H. Можно показать, что компоненты вектора uÎH являются соответственно элементами пространств: u1,u1,u2,u2Î Wo2(1)(W), u3=u3=wÎWo2(2)(W) и, более того, соответствующие нормы двух пространств H и W=Wo2(1)(W)´Wo2(1)(W)´Wo2(2)(W) эквивалентны.
Определение 1. Замыкание множества гладких вектор-функций, зависящих от пространственных координат и времени и удовлетворяющих условиям (3), в норме, индуцированной скалярным произведением
(u,
du)W(0;T)
=ò0
T
{rh
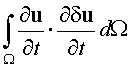 +
òW [cijklqkl
dqij +
+
òW [cijklqkl
dqij +
+h3/12
cijklrkl
drij]dW}
dt,
называется пространством W(0;T). Его подпространство, полученное замыканием множества вектор-функций, удовлетворяющих условию u(x, T) = 0, назовем W0(0;T).
Для полной постановки задачи задаются начальные данные:
u|t=0= u0(x) , ¶u(t)/¶t|t=0= u1(x). (4)
Теперь сформулируем постановку начально-краевой динамической задачи нелинейной теории непологих оболочек.
Определение 2. Вектор-функция u(t)ÎW(0;T), удовлетворяющая уравнению (2) при любом duÎ W0(0;T) и первому из начальных условий (4) в следующем смысле: òW|u(t) - u0 |2dW ® 0 при t®0, называется обобщенным решением задачи динамики непологой вязкоупругой оболочки с жестко защемленным краем.
Следует сказать, что при решении соответствующей задачи методом конечного элемента фактически приближенно определяется решение именно в такой формулировке, а не классическое решение, когда от него требуется наличие всех входящих в дифференциальные уравнения производных.
Предположим, что u0(x), u1(x)Î H и F iÎL2(W´[0; T]).
Сейчас мы можем сформулировать теорему разрешимости.
Теорема. При выполнении всех указанных выше условий при любом конечном T существует обобщенное в смысле Определения 2 решение задачи динамики вязкоупругой непологой оболочки с жестко защемленным краем.
Доказательство теоремы существования проводится в три этапа: 1) построение уравнений метода Бубнова-Галеркина (модификацию которого применительно к задачам динамики в западной литературе упорно называют методом Фаэдо-Галеркина); 2) доказательство разрешимости уравнений на каждом этапе приближений, основанное на получении глобальной априорной оценки; 3) обоснование предельного перехода в уравнениях метода Бубнова-Галеркина с доказательством, что предел приближенных решений является обобщенным решением задачи.
Само доказательство в силу его громоздкости здесь не приводится. Сейчас нас интересует, каковы выводы, следующие из полученного доказательства для численного решения задач методом Бубнова-Галеркина, включающим в себя различные варианты метода конечного элемента, используемого в программах типа ANSYS.
Разрешимость конечномерных уравнений метода Бубнова-Галеркина в каждом приближении доказывается относительно несложно. Отметим, что подобное доказательство разрешимости уравнений метода Бубнова-Галеркина получается и для многих других задач, где разрешимость задач в целом еще не установлена. Такова ситуация для различных вариантов задач статики и динамики нелинейной теории упругости, пространственных уравнений Навье-Стокса и многих других. Таким образом, теоретическая возможность нахождения некоего приближения оказывается обоснованной. Тот факт, что можно численно найти решение задачи при любых нагрузочных членах, многими расчетчиками трактуется как свидетельство, что сама первоначальная задача всегда разрешима. Однако это не всегда так. Даже если имеется доказательство теоретической сходимости приближенных решений к точному, то практически такую сходимость приближений к точному решению осуществить невозможно. Этому препятствует конечность разрядной сетки компьютера. В свою очередь это приводит к тому, что имеется некоторый предел достижимой точности численных решений краевых задач, который не может быть превышен принципиально на данном компьютере. Обычный метод практического «обоснования» сходимости численного метода, когда численное решение проводится с большим числом базисных элементов или точек разбиения области и т.п., затем приближение более высокого порядка сравнивается с предыдущим, а их близость служит критерием сходимости метода, может лишь свидетельствовать лишь о том, что результат в следующих приближениях изменится не слишком сильно. Таким образом, этот практический прием не является обоснованием сходимости численного метода, которая должна исследоваться отдельно. Доказательство теорем разрешимости использованным нами способом обосновывает сходимость проекционных методов и дает реальную базу для утверждения о близости компьютерных решений к истинным. Это же доказательство указывает также и характер сходимости приближений.
Литература
1. Koiter W.T., On the nonlinear theory of thin elastic shells. I; Proc. Kon. Ned. Akad. Wetensch., 1966, B 69, pp. 1-54
2. Ворович И.И., Математические проблемы нелинейной теории пологих оболочек; М., Наука, Гл. ред. физ.-мат. лит-ры, 1989, 374 с.;
англ. перев.: I.I. Vorovich, Nonlinear theory of shallow shells, Springer-NY, 1998, 1-388