Complex Problems

i. 8 Queens

This is a commonly known chess problem...

The Question: In how many ways can you arrange 8 queens on a standard chessboard in such a way that none of them is attacking any other?

ii. Names & Numbers

Thanks to Mike and Ruth VanderMeer from Canada, Le Monkey can present you the following names and numbers puzzle:

Four words add up to a fifth word numerically:

     mars
    venus
   uranus
   saturn
 -------- +
  neptune

Each of the ten letters (m, a, r, s, v, e, n, u, t, and p) represent a unique number from the range 0 .. 9. Furthermore, numbers 1 and 6 are being used most frequently.

The Question: What numbers does neptune equal?

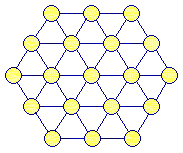
iii. Nineteen Numbers Net

This is the toughest number net on our site! It has nineteen circles that have to be filled with the numbers 1 upto (and including) 19. These numbers have to be placed in such a way that all numbers on any horizontal row and any diagonal line add up to the same sum.

Warning: there are many horizontal and diagonal lines, which have a different number of circles (3, 4, or 5), nevertheless all these sums have to be equal!

The Question: How should the nineteen numbers be placed in the net?

iv. Roulette

A well known roulette trick is doubling the bet if one loses. But consider this roulette problem to be limited to a maximal number of consecutive bets.

The Question: What is the behavior of the expectation (E(n)) for a limited roulette problem?

v. Cash for a Car

Thanks to Lucas Jones Le Monkey can present you the following puzzle:

A man is going to an Antique Car auction. All purchases must be paid for in cash. He goes to the bank and draws out $25,000.

Since the man does not want to be seen carrying that much money, he places it in 15 evelopes numbered 1 through 15. Each envelope contains the least number of bills possible of any available US currency (i.e. no two tens in place of a twenty).

At the auction he makes a successful bid of $8322 for a car. He hands the auctioneer envelopes number(s) 2, 8, and 14. After opening the envelopes the auctioneer finds exactly the right amount.

The Question: How many ones did the auctioneer find in the envelopes?

vi. Ladder Alley

In an alley two ladders are placed cross-wise. The lengths of these ladders are resp. 2 and 3 meters. They cross one another at one meter above the ground.

The Question: What is the width of the alley?

vii. Cat & Mouse

Four white pieces are placed on one side of a chess board, and one black piece is placed at the opposite site. The game is played by the following rules:

Black wins if it reaches the opposite side.

White wins if it blocks black in such a way that black can not do any legal move anymore.

Only diagonal moves (of length 1) are allowed.

White only moves forward.

Black can move backward and forward.

Black may make the first move, then white make a move, and so on...

The Question: Is this game computable (i.e. is it possible to decide beforehand who wins the game, no matter how hard his opponent tries to avoid this)?

viii. Car Parking

A street of length L is randomly filled with cars (one by one), where the length of a car is the unity of L (i.e. 1).

The Question: What is the expectation for the number of cars that can be parked until the street is filled?

Hosted by www.Geocities.ws