Trigonometric
Functions of a General Angle
Previously, we defined the trigonometric functions of an acute angle.
The definitions were based on the various ratios of the sides of a right triangle.
Now we define the trigonometric functions of any angle, no restrictions on the
size
or the sign (positive or negative) of the angle.
These general definitions are given within the context of the Cartesian coordinate
system
of analytic geometry.
Give an arbitrary angle,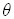 
,
with its vertex at the origin of a cartesian coordinate system
and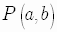 
any point 
units from the origin on the terminal side the angle ,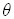
the six trigonometric functions of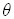
are defined as follows.
Trigonometric
Functions for an Arbitrary Angle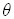
is
an arbitrary point on the terminal side of ,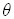
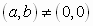
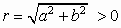
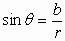
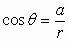
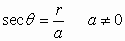
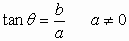
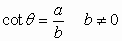
In the above definition the right triangle formed by dropping a perpendicular
from
to the horizontal axis is called the reference triangle associated with
the angle .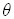
See
Examples 1 - 2, pages 437 - 438, of the textbook.
Trigonometric
Functions with Real Number Domains
For any real number x, we can think of x as being x radians,
so we can define the trigonometric functions for any real number x.
sin x = sin (x in radians) csc x = csc (x in radians)
cos x = cos (x in radians) sec x = sec (x in radians)
tan x = tan (x in radians) cot x = cot (x in radians)
In other words, the above definitions define the trigonometric functions
with domains that consist of all the real numbers. This enables us to evaluate
the trigonometric functions of quantities that are not necessarily angles and
so opens the use of trigonometric functions to a far wider range of applications.
See
Examples 3 - 4, pages 439 - 441, of the textbook.
The previous trigonometric identities now are generalized for real number domains.
Reciprocal
Identities
For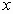 
any real number
or angle in degree or radian measure:
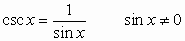
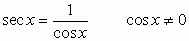
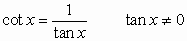
Calculator
Evaluation
Set the calculator in degree mode when evaluating trigonometric functions of angles
in degree measure.
Set the calculator in radian mode when evaluating trigonometric functions of angles
in radian measure
or trigonometric functions of real numbers.
See
Example 3, page 439, of the textbook.
Summary
of Sign Properties of the Trigonometric Functions
The
signs of the trigonometric functions of an angle vary as the angle
progresses
through the quadrants of the Cartesian coordinate system.
Quadrant
I Quadrant
II
Quadrant III
Quadrant IV
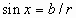
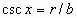
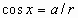
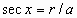
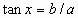
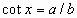
top
next
Exact Values for Special Angles and Real Numbers