Inferencia lógica

La inferencia lógica es un mecanismo de derivación sintáctica que a partir de un conjunto dado de fórmulas permite derivar nuevas fórmulas, utilizando operaciones que se denominan reglas de inferencia.

El conjunto inicial de fórmulas son sentencias válidas en un cierto lenguaje y se les llama axiomas. Los axiomas junto a las reglas de inferencia constituyen lo que Frege denomina un sistema formal.

Mediante la inferencia lógica, es posible demostrar fórmulas sin necesidad de considerar interpretación alguna. Una prueba será una derivación en el sistema formal, y la utilidad de la misma surgirá de ciertas propiedades de las reglas de inferencia, llamadas de completitud, que serán presentadas más adelante.

A los efectos de esta presentación, las fórmulas a considerar serán las que satisfagan los requerimientos sintácticos que fueron introducidos en 3.1. En una primera instancia no se considerarán los predicados con variables, para estudiar en detalle los mecanismos de demostración. La influencia de la presencia de variables será considerada en la sección 3.4.

Una de las reglas de inferencia más conocida, y que forma parte de numerosos sistemas formales es la denominada modus ponens. Ella se basa en el conector de implicación lógica « $\rightarrow$».

Definición 3.6 (Modus ponens)
De las fórmulas $A$ y $A\rightarrow B$, se puede inferir $B$, lo que usualmente se escribe de la siguiente forma:

$$\begin{array}{lll} A \\ A & \rightarrow & B \\ \hline B \end{array}$$

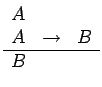
En lo que sigue se presentan una serie de definiciones que serán utilizadas posteriormente.

En un sistema formal, un paso de inferencia corresponde a la aplicación de una regla para inferir una nueva fórmula.

Definición 3.7 (Demostración)
Una demostración será una sucesión $F_1, F_2, \ldots, F_n$ de fórmulas del lenguaje, tal que todo $F_i$ es un axioma, o se obtiene de las fórmulas anteriores en la sucesión por la aplicación de alguna regla de inferencia.

Definición 3.8 (Teorema)
Una fórmula $F$ es un teorema si existe una demostración en la que $F$ es el último término de la sucesión.

Notación 2
Si $F$ es un teorema se notará $\vdash F$

Definición 3.9 (Deducción lógica)
Sea $F$ una fórmula y $R$ un conjunto de fórmulas de una cierta teoría, se dice que $F$ es deducible lógicamente a partir de $R$, y se escribe $R \vdash F$, si existe una sucesión de fórmulas $F_1, F_2, \ldots, F_n$ tal que $F = F_n$ y cada $F_i$ es

• un axioma de la teoría
• o una fórmula de $R$
• o deducible de un fórmula precedente en la sucesión.

Las fórmulas de $R$ se llaman hipótesis.

Notación 3
Si $A$ es deducible lógicamente de $R$ se notará: $R \vdash A$

Una propiedad importante, que será utilizada más adelante, es la siguiente:

Definición 3.10 (Consistencia)
Un sistema formal, en el que existe el símbolo de la negación «$\neg$» se dice que es consistente si no existe una fórmula $F$ en el sistema tal que pueda deducirse $F$ y $\neg F$. Un sistema se llama inconsistente en caso contrario.

Resumiendo los conceptos presentados, se han introducido dos alternativas vinculadas con la idea de prueba de fórmulas. En primer lugar se tiene el concepto de satisfacción lógica, que tiene connotaciones semánticas, y que en definitiva es la que interesa cuando se intenta dar un significado a la ejecución de un programa en lógica. Sin embargo no parece evidente encontrar mecanismos automatizables para la prueba, que consideren todas las interpretaciones posibles, tal como se necesita a partir de la definición de satisfacción lógica. En segundo lugar se presentó el mecanismo de inferencia lógica, que basado en elementos sintácticos, permte definir derivaciones entre fórmulas, e introducir el concepto de teoremas, a partir de un conjunto de axiomas, y de las reglas de inferencia utilizadas. Esta alternativa parece ser más útil desde un punto de vista informático, si se encuentran procedimientos que implementen las reglas del sistema.

La vinculación entre ambas alternativas surge de la propiedad de completitud de las reglas de inferencia.

Definición 3.11 (Completitud)
Sea un programa en lógica $P$, y una cláusula $p$ que corresponde a una invocación del programa $P$.

Sea $Q$ una regla de inferencia.

Se dice que $Q$ es completa si se cumple que:

$p$ es deducible lógicamente de $P$, utilizando $Q$ ssi $p$ es consecuencia lógica de $P$

O sea $P \vdash p \Leftrightarrow P \models p$

Nota. 1
En la literatura se encuentra que frecuentemente se le llama robustez (englishsoundness) a la parte «sólo si» de la propiedad definida, y completitud a la parte «si» de la misma.

Según la definición anterior, si se dispone de reglas de inferencia que cumplan con la propiedad de completitud, alcanza con demostrar la deducibilidad de una fórmula para demostrar que la misma es consecuencia lógica del programa.

Dentro del área de automatización de pruebas mediante el concepto de deducibilidad, un aporte importante es debido a Robinson, quien introdujo la llamada regla de resolución.

Definición 3.12 (Regla de Resolución)
Sean $A_1, \ldots, A_n$ y $B_1, \ldots, B_m$ símbolos predicativos, la regla dice:

$$\begin{array}{l} \neg(A_1, \ldots, A_k, \ldots, A_n) \\ A_k \le... ...\neg(A_1, \ldots, A_{k-1}, B_1, \ldots, B_m, A_{k+1}, \ldots, A_n) \end{array}$$

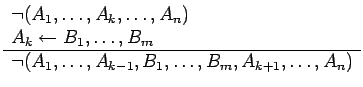
De la definición puede observarse que la regla de resolución resulta particularmente adaptada para los programas en lógica. Una invocación o pregunta, corresponde a fórmulas del primer tipo, y las reglas o cláusulas del programa corresponden al segundo tipo. La aplicación de las reglas introduce una nueva cláusula producto de la anulación o cancelación del predicado $A_k$.

Como casos particulares de a regla de resolución se pueden considerar los siguientes:

a)

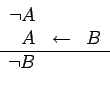
$$\begin{array}{rll} \neg A & & \\ A & \leftarrow & B \\ \hline \neg B \end{array}$$

llamada modus tollens.

b)

$$\begin{array}{rr} \neg A \\ A & \qquad\mbox{o «} A \left... ...w .\mbox{» según la sintaxis.}\\ \cline{1-1} [] \end{array}$$

que significa que se ha concluído con una contradicción.

El aporte realmente importante de la regla de resolución surge del siguiente teorema.

Teorema 3.1 (Completitud de la resolución)   La regla de resolución es completa.

En virtud de lo anterior es posible concebir un sistema de demostración automática que evalúe los programas en lógica, mediante la aplicación reiterada de la regla de resolución, tratando de demostrar la deducibilidad lógica de la invocación.

Una manera de realizar la prueba es la llamada prueba por contradicción o por reducción al absurdo, que se basa en el siguiente teorema.

Teorema 3.2   Sea $F$ una fórmula y $R$ un conjunto de fórmulas. $F$ es deducible lógicamente a partir de $R$, ssi el conjunto formado por $R$ con $\neg F$ es inconsistente.

O sea,

$$R \vdash F \Leftrightarrow R \cup \{ \neg F \}$$    es inconsistente$$$$

Las definiciones y teoremas presentados son la base para comprender el significado de los programas en lógica, y de la ejecución de los mismos. Las demostraciones se han omitido para abreviar la exposición. El lector interesado puede encontrar una presentación formal y completa de estos temas en el libro de E. Mendelson [Men64], y un buen resumen de los mismos en el primer capítulo de la tesis de R. Caferra [Caf82].

Es posible ahora presentar un modelo sobre la evaluación de un programa en lógica. De la definición sintáctica se sabe que los tres tipos de reglas posibles en programación en lógica son:

$$\begin{array}{lcll} A & \leftarrow & . & \mathrm{(I)}\\ A ... ... & \leftarrow & B_1, \ldots, B_m & \mathrm{(III)} \end{array}$$

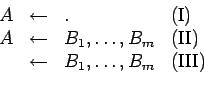
Las reglas tipo (I) y (II) corresponden a las fórmulas que conforman el programa: en el sistema lógico representan los axiomas. Las fórmulas de tipo (III) son las invocaciones de ejecución, y si se recuerda su interpretación como cláusulas de Horn, representan a la negación de la conjunción de los $B_i$, tal como aparece en la fórmula (IX) vista anteriormente.

El modelo se presenta fácilmente mediante un ejemplo.

Ejemplo. 1
Sea el programa $P$:

$$\begin{array}{lcll} A & \leftarrow & . & (1)\\ B & \leftarrow &... ...)\\ C & \leftarrow & D, A. & (4)\\ F & \leftarrow & C, B. & (5) \end{array}$$

y la invocación dada por la fórmula $p$:

$$\begin{array}{lcll} & \leftarrow & F. & (6) \end{array}$$

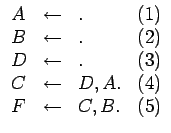
La intención es probar que

$$P \models F$$

lo que se realiza demostrando mediante la regla de resolución que:

$$P \vdash F$$

Realizando la demostración por el absurdo, el procedimiento será probar que:

el conjunto $P \cup \{\neg F\}$ es inconsistente.

Pero la fórmula $p$ es $\neg F$, por lo que se debe demostrar es que:

el conjunto $P \cup \{ p \}$ es inconsistente

Para demostrar que el conjunto 1-6 es inconsistente se va aplicando resolución para inferir nuevas cláusulas. Por ejemplo:

      De (5) y (6) 		 se infiere 		 
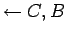$\leftarrow C, B$ (7)


De (4) y (7) 		 se infiere 		 
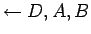$\leftarrow D, A, B$ (8)


De (3) y (8) 		 se infiere 		 
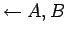$\leftarrow A, B$ (9)


De (1) y (9) 		 se infiere 		 
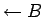$\leftarrow B$ (10)


De (2) y (10) 		 se infiere 		 
$\leftarrow [\,]$ (11)    

El paso (11) indica que se ha inferido el conjunto vacío. Esto surge de considerar las reglas (2) y (10). La primera afirma $B$ y la segunda afirma $\neg B$, por lo tanto el sistema es inconsistente.

De la evaluación del ejemplo surgen las siguientes consideraciones:

1. Una invocación corresponde a una cláusula de tipo (III) con un solo símbolo predicativo.

2. Las nuevas cláusulas que se van infiriendo corresponden a clásulas de tipo (III), donde cada uno de los símbolos predicativos que aparecen en ellas corresponderán a pasos de inferencia que deberán ser realizados.

3. Cuando la resolución se aplica entre una cláusula de tipo (II) y una $b$ de tipo (III), la cláusula obtenida tiene los símbolos de $b$, menos el símbolo consecuente de $a$, que ha sido sustituído por el conjunto de sus antecedentes. Aquí la cláusula obtenida tiene más, o la misma cantidad de símbolos que $b$.

4. La estrategia de la demostración consiste en buscar inferir la cláusula vacía ($[\,]$).

Hosted by www.Geocities.ws