El lenguaje que se utiliza en la programación en lógica proviene de la lógica de predicados de primer orden.
Se dispone de:
Cada símbolo funcional y predicativo tiene asociado un número entero que corresponde a su aridad.
Como convención se adoptará que los átomos estarán formados por caracteres en minúsculas y números, por ejemplo:
a, b, raquel, 1, 3200, paris, caracas
Las variables se denotarán utilizando letras mayúsculas:
X, Y, Z, ...
Para los símbolos funcionales se usarán también letras minúsculas, lo que no ofrece ambigüedad con los átomos, debido a su diferenciada ubicación sintáctica. Los símbolos predicativos serán denotados usando letras mayúsculas.
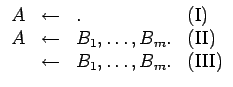
siendo
![]() predicados.
predicados.
Mediante el concepto de términos, y utilizando los símbolos funcionales es posible estructurar la información a ser manipulada por los programas en lógica. Por ejemplo, si se tiene:
empleado( jaime, 32, 1827 )
con empleado símbolo funcional, y jaime, 32 y 1827, átomos, el significado de dicho término podría ser que jaime es un empleado que tiene 32 años, y que su número interno es 1827. La interpretación de cada uno de los átomos presentes surge entonces de su posición en el término, lo que equivale a asignar significado a los dominios del símbolo funcional. Si se desea un mayor poder de expresión, esto puede lograrse agregando nuevos símbolos funcionales (unarios) como en el ejemplo:
empleado( nombre(jaime), edad(32), numero(1827) ).
Un símbolo funcional distinguido, y que será denotado con un punto («.») permite definir expresiones simbólicas (árboles binarios). Estas estructuras, llamadas S-expresiones, fueron introducidas para los lenguajes funcionales como LISP. Su sintaxis es muy simple:
S-expresión ::= átomo
S-expresión ::= "[" S-expresión "." S-expresión "]"
Mediante el símbolo funcional «.», y admitiendo para él una notación infija, se obtienen las S-expresiones como términos del lenguaje. Así por ejemplo se pueden escribir los términos:
[a.[b.c]], [[[x.t].y].[r.[o.p]]]
los que visualizados como árboles binarios tendrían la siguiente representación:
* *
/ \ / \
/ \ / \
a * * *
/ \ / \ / \
/ \ / \ / \
b c * v r *
/ \ / \
/ \ / \
x t o p
Para la definición recursiva de los árboles es necesario
considerar un elemento particular que representa el árbol
vacío y que se denotará con «[]» (también se le
representa como NIL). Con dicho elemento es posible
considerar un caso particular de árboles binarios, que corresponderá
al concepto de listas. Una lista, o sucesión de elementos, por
ejemplo
![]() , tendrá como representación al siguiente árbol
binario: [a.[b.[c.[d.[]]]]].
, tendrá como representación al siguiente árbol
binario: [a.[b.[c.[d.[]]]]].
En base a las estructuras de árboles recién vistas, se puede diseñar
un programa lógico cuyo cometido sea el de concatenar dos listas.
Este es un problema clásico para resolver en programación funcional,
donde el objetivo es escribir una función que recibiendo como
argumentos dos listas, como por ejemplo ![]() y
y ![]() , evalúe
como resultado la concatenación de las mismas. En el ejemplo sería:
, evalúe
como resultado la concatenación de las mismas. En el ejemplo sería:
![]() .
.
En programación en lógica el programa es el siguiente:
CONCAT( [], X, X ) <- .
CONCAT( [X.L], Y, [X.Z] ) <- CONCAT( L, Y, Z ).
De acuerdo a lo que se planteó en la sintaxis, este programa es un conjunto de dos reglas, que tal como se vió en la introducción definen una relación:
CONCAT en (listas) x (listas) x (listas).
En realidad el problema propuesto corresponde a una función de:
(listas) x (listas) -> (listas).
si se interpreta que el tercer argumento corresponde a la concatenación del primero con el segundo, pero en la programación en lógica sólo se pueden representar relaciones.
Cabe destacar aquí que las variables que aparecen en el programa tienen como alcance cada una de las reglas. Es decir que la X en la primera regla es diferente a la de la segunda.
Varias pueden ser las formas de leer el programa CONCAT. La primera regla indica que la concatenación de la lista vacía con cualquier listas X, da como resultado la misma lista X. Esta regla expresa además que éste es un hecho sin condicionantes, ya que no aparecen predicados a la derecha del símbolo «<-». La segunda regla puede leerse de derecha a izquierda. Si adoptamos la notación de «*» para el operador de concatenación de listas, la regla representa:
lo que equivale al paso inductivo de una definición recursiva de la relación CONCAT.
Un primer elemento a destacar de los programas en lógica, es su carácter declarativo. Al analizar el programa CONCAT, se constata que el mismo se parece mucho más a una definición formal que a una descripción algorítmica. Uno de los problemas más complejos de la programación tradicional es el de estableceer mecanismos formales que permitan especificar el problema a resolver, y que además sirvan para determinar si un cierto algoritmo dado verifica las condiciones del problema. Dicho de otra manera, la dificultad consiste en vincular la especificación de un problema donde se define qué significa, con un algoritmo para resolverlo donde se expresa cómo hacerlo. La brecha entre el qué y el cómo se reduce enormemente en la programación lógica, como puede constatarse en los ejemplos presentados, aún cuando existen dificultades al introducir los componentes de control, tal como se verá en el capítulo siguiente.
Una segunda característica muy importante de la programación lógica, se
basa en sus aspectos relacionales, que la diferencian de los otros
paradigmas que asocian funciones a los programas. Tanto en la
programación imperativa tradicional como en la programación funcional,
queda perfectamente establecido la dependencia entre datos de entrada y
resultados de la ejecución. El flujo de información es un elemento de
diseño, y un cambio del mismo implica una modificación importante del
programa. Supóngase por ejemplo que se dispone de un programa en PASCAL
(o en ADA, o en cualquier lenguaje clásico), que computa la función
concatenación en el sentido que recibe dos listas (X y
Y) como datos de entrada, y devuelve como resultado la lista
(Z) obtenida de concatenar la primera con la segunda (![]() ).
Si en un momento dado resulta necesario cambiar ligeramente las
condiciones del problema, por ejemplo dadas dos listas (X y
Z), se desea calcular una tercera lista (Y) tal que
esta última concatenada a la derecha con el primer argumento dé como
resultado el segundo argumento (
).
Si en un momento dado resulta necesario cambiar ligeramente las
condiciones del problema, por ejemplo dadas dos listas (X y
Z), se desea calcular una tercera lista (Y) tal que
esta última concatenada a la derecha con el primer argumento dé como
resultado el segundo argumento (![]() ), entonces se debe proceder a
realizar cambios sustanciales en el programa original. El aspecto
relacional de la programación en lógica le da un carácter de
reversibilidad a sus argumentos, y el mismo programa permite, en
general, todas las combinaciones posibles de dependencias de
entrada/salida.
), entonces se debe proceder a
realizar cambios sustanciales en el programa original. El aspecto
relacional de la programación en lógica le da un carácter de
reversibilidad a sus argumentos, y el mismo programa permite, en
general, todas las combinaciones posibles de dependencias de
entrada/salida.
Si se considera el programa CONCAT ya visto, las siguientes son utilizaciones posibles del mismo:
<- CONCAT ( (a b), (c d), Z ).
la ejecución da como resultado
Z = (a b c d).
<- CONCAT ( (a b), Y, (a b c d) ).
la ejecución da como resultado
Y = (c d).
<- CONCAT ( X, Y, (a b) ).
la ejecución da como resultados
X = () , Y = (a b).
X = (a) , Y = (b).
X = (a b) , Y = ().
donde «()» representa a la lista vacía (o árbol vacío «[]»).
La sintaxis de la programación en lógica presentada proviene de la correspondiente a la lógica de primer orden. En el lenguaje de dicha lógica se utilizan los vocabularios ya mencionados, así como conectores lógicos y los cuantificadores (universal y existencial). Con miras a unificar el tratamiento de las fórmulas bien formadas de la lógica de primer orden se han definido diversas formas normales. Entre ellas resulta de particular interés la llamada forma clausal de Skolem, cuyo formato general es el siguiente:
donde los ![]() y los
y los ![]() son predicados en el sentido de la
definición vista.
son predicados en el sentido de la
definición vista.
En dicho formato no aparecen los cuantificadores existenciales, y que
los predicados están relacionados únicamente por el conector ![]() . La
distinción en utilizar los símbolos
. La
distinción en utilizar los símbolos ![]() y
y ![]() , tiene el propósito de
destacar que los segundos están prefijados por el símbolo de negación.
, tiene el propósito de
destacar que los segundos están prefijados por el símbolo de negación.
Se puede demostrar que para toda fórmula bien formada del cálculo de predicados, existe una fórmula en forma clausal de Skolem tal que ambas tienen las mismas propiedades de satisfactibilidad semántica.
Por propiedades bien conocidas de los conectores lógicos es fácil ver que la fórmula (IV) es equivalente a la siguiente:
Resulta evidente que las cláusulas de Horn conforman un subconjunto estricto del lenguaje del cálculo de predicados de primer orden.
De acuerdo a la definición son tres las posibilidades para las cláusulas de Horn:
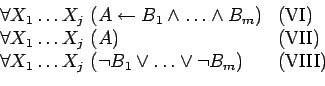
que es equivalente a:
Dado que en la forma clausal los únicos cuantificadores que aparecen
son los universales, pueden entonces ser suprimidos, interpretando
toda cláusula como clausurada universalmente. Al proceder de esta
manera se puede reconocer que los tres tipos posibles de cláusulas
para la programación en lógica (I, II, y III) corresponden a
variaciones sintácticas de las formas VI, VII y IX. De esta forma es
posible dar una interpretación a cada tipo de cláusulas. Las de tipo
(I) corresponden a la afirmación del predicado ![]() por parte del
programador. Las del tipo (II) representan los hechos condicionales:
por parte del
programador. Las del tipo (II) representan los hechos condicionales:
![]() son predicados ciertos, entonces
son predicados ciertos, entonces ![]() también es cierto.
Finalmente las cláusulas de tipo (III) corresponden a las invocaciones
de ejecución del programa, o si se prefiere a las interrogaciones de
las relaciones definidas: ¿existen valores de las variables
también es cierto.
Finalmente las cláusulas de tipo (III) corresponden a las invocaciones
de ejecución del programa, o si se prefiere a las interrogaciones de
las relaciones definidas: ¿existen valores de las variables
![]() tales que con dichos valores los predicados
tales que con dichos valores los predicados
![]() son ciertos?
son ciertos?