Elliptic Axes Calculator (x/a) ² + (y/b) ² = 1 Scope: First Quadrant x1 = y1 = x2 = y2 = Ratio of Axes ... a/b = on x-axis ... 2a = on y-axis ... 2b = ± on Major Axis ... Foci =

Roof with Elliptic Footprint Calculator




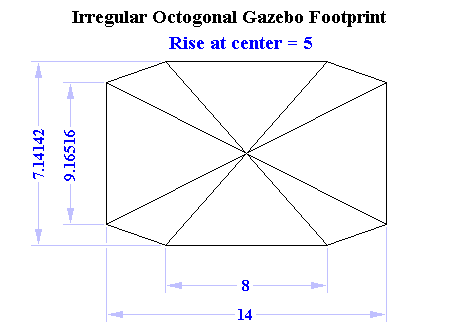
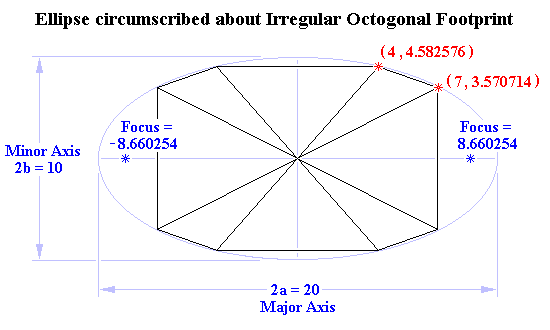
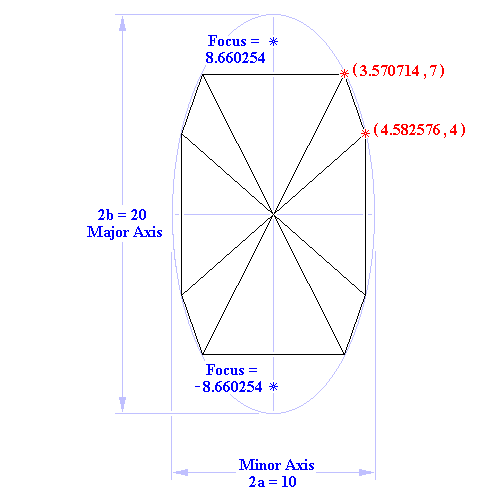
An Example Solution

From the dimensions of the gazebo footprint ... ( x1, y1 ) = ( 4, 4.582576 ) ( x2, y2 ) = ( 7, 3.570714 ) Intercept form of the Equation of the Ellipse ... (x/a)² + (y/b)² = 1 Substituting for x and y ... (4/a)² + (4.582576/b)² = 1 (7/a)² + (3.570714/b)² = 1 Squaring the terms ... 16/a² + 21/b² = 1 49/a² + 12.75/b² = 1 Multiplying all terms by a²b² to eliminate the denominators ... 21a² + 16b² = a²b² 12.75a² + 49b² = a²b² Since both points are on the same ellipse and the right hand sides of both equations equal a²b² , the left hand sides of the equations are equal to one another ... 21a² + 16b² = 12.75a² + 49b² 8.25a² = 33b² a² = 33b²/8.25 = 4b² Taking the square root of both sides of the equation ... a = 2b Substituting for a in either of the original equations ... 16/(2b)² + 21/b² = 1 16/(4b²) + 21/b² = 1 16/(4b²) + 84/(4b²) = 1 (16 + 84)/(4b²) = 1 (16 + 84)/4 = b² b² = 100/4 = 25 Taking the square root of both sides of the equation ... b = 5 Minor Axis of the ellipse on the y-axis ... Minor Axis = 2b = 10 Since a = 2b ... a = 10 Major Axis of the ellipse on the x-axis ... Major Axis = 2a = 20 Foci = Ö(a² – b²) ... Ö(10² – 5²) = ±8.660254 Intercept form of the Equation of the Ellipse ... (x/10)² + (y/5)² = 1 Cartesian Equation of the Ellipse ... x² + 4y² = 100