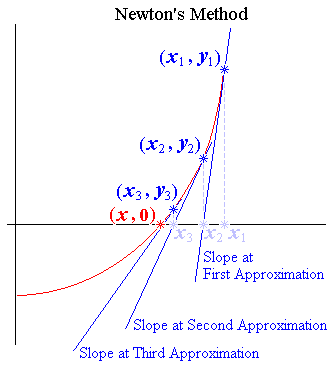
Newton's Method
|
Solve the roots of the equation
y = x ² – 5200
73 ² = 5329, let x = 73 for a trial value At x = 73 y = 73 ² – 5200 = 129 The slope of the equation y = x ² – 5200 at any station : dy/dx = d(x ² – 5200)/dx = 2x At x = 73 , Slope = 2 × 73 = 146 Equation of tangent at P ( x , y ) = ( 73 , 129 ) : 146 = ( y – 129 ) / ( x – 73 ) 146x – 10658 = y – 129 y = 146x – 10529 When y = 0 the x-intercept of the tangent is : x = 10529/146 = 72.11644 Testing the result : 72.11644 ² = 5200.78092 Let 72.11644 be the new trial value At x = 72.11644 y = 72.11644 ² – 5200 = .78092 At x = 72.11644 , Slope = 2 × 72.11644 = 144.23288 Equation of tangent at P ( x , y ) = ( 72.11644 , .78092 ) : 144.23288 = ( y – .78092 ) / ( x – 72.11644 ) 144.23288x – 10401.56184 = y – .78092 y = 144.23288x – 10400.78092 When y = 0 the x-intercept of the tangent is : x = 10400.78092/144.23288 = 72.11103 Testing the result : 72.11103 ² = 5200.00065 |
Binomial Series for Rational Exponents
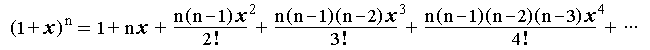
|
Find the square root of 5200
The closest square to 5200 is 72 × 72 = 5184 5200 = 5184 + 16 5200½ = ( 5184 + 16 )½ = 5184½ × ( 1 + 16/5184 )½ = 72 × ( 1 + 16/5184 )½ The terms in the parentheses are in the correct form, with x = 16/5184 and n = 1/2 : 72 × ( 1 + 16/5184 )½ = 72 × ( 1 + 1/2 × 16/5184 + [ 1/2 × -1/2 × 16/5184 × 16/5184 ] / 2 + [ 1/2 × -1/2 × -3/2 × 16/5184 × 16/5184 × 16/5184 ] / [ 3 × 2 ] + ... ) = 72 × ( 1 + 1/648 – 1/839808 + 1/544195584 – ... ) = 72.11103 ... checking the result : 72.11103 ² = 5200.00065 Since x = 16/5148 = 1/324 is small the series converges rapidly. Two terms would still return the same accuracy to five decimal places and : 72 × ( 1 + 1/648) = 72.11189 ... accurate to two decimal places |