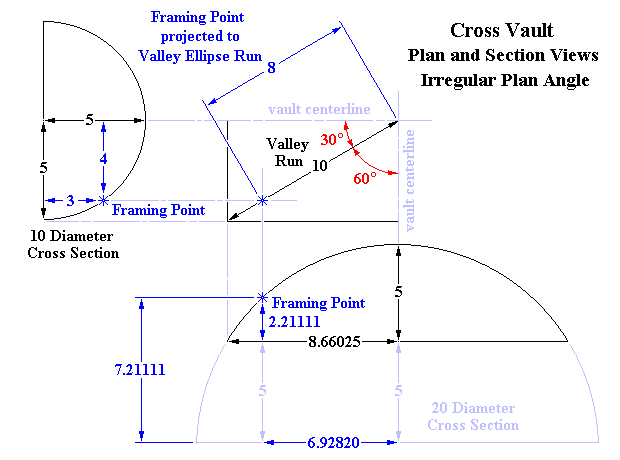
10 Diameter Semi-Circle intercepts 20 Diameter Circle Section
Plan Angles for all calculations are as per the diagram
|
Vault Height = 5
For Height = 5 : 20 Diameter Circle Section Width 2 = 10 2 – 5 2 = 75 20 Diameter Circle Section Width = 8.66025 Semi-Circle Plan Angle = arctan (5 ÷ 8.66025) = 30° 20 Diameter Circle Section Plan Angle = arctan (8.66025 ÷ 5) = 60° Valley Ellipse Run = 5 ÷ sin 30° = 10 Equation of Valley Ellipse = x 2 + 4 y 2 = 100 Semi-Major Axis = 10 Semi-Minor Axis = 5 Major Axis = 20 Minor Axis = 10 Let the 10 Diameter Circle horizontal dimension = 4 For Width = 4 : Height of 10 Diameter Circle 2 = 5 2 – 4 2 = 9 Height of 10 Diameter Circle = 3 Corresponding horizontal dimension of the 20 × 10 Valley Ellipse = 4 ÷ sin 30° = 8 For Width = 8 : Height of 20 × 10 Valley Ellipse 2 = ( 100 – 8 2 ) ÷ 4 = 9 Height of 20 × 10 Valley Ellipse = 3 Projection of dimension to 20 Diameter Circle = 8 × sin 60° = 6.92820 For Width = 6.92820 : Height of 20 Diameter Circle 2 = 10 2 – 6.92820 2 = 52 Height of 20 Diameter Circle = 7.21111 Height of 20 Diameter Circle Section = 7.21111 – 5 = 2.21111 ... a fatal contradiction since the HEIGHTS at CORRESPONDING HORIZONTAL DIMENSIONS must be EQUAL Let the 20 Diameter Circle Section height = 3 Height of 20 Diameter Circle = 3 + 5 = 8 Width of 20 Diameter Circle 2 = 10 2 – 8 2 = 36 Width of 20 Diameter Circle = 6 ... corresponding run in plan = 6.92820 The POINT on the SURFACE of the VAULT does not align with the CORRESPONDING POINT in PLAN |
|
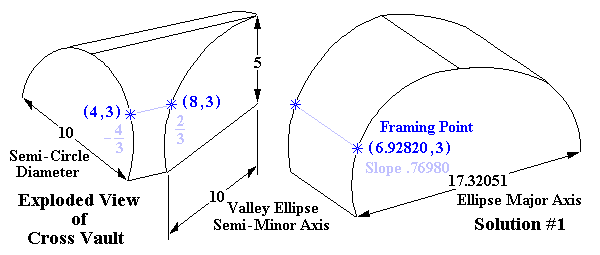
Solution #1: Make the 20 Diameter Circle Section a Semi-Ellipse
Semi-Major Axis = 8.66025 Semi-Minor Axis = 5 Major Axis = 17.32051 Minor Axis = 10 Equation of Ellipse = x 2 + 3 y 2 = 75 For 20 × 10 Valley Ellipse horizontal dimension = 8 : Projection to 17.32051 × 10 Ellipse = 8 × sin 60° = 6.92820 Height of 17.32051 × 10 Ellipse 2 = ( 75 – 6.92820 2 ) ÷ 3 = 9 Height of 17.32051 × 10 Ellipse = 3 HEIGHTS at CORRESPONDING HORIZONTAL DIMENSIONS are EQUAL |
|
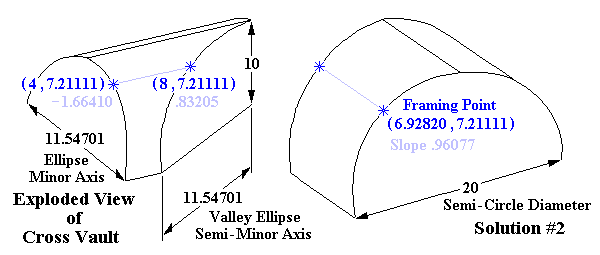
Solution #2: Make the 10 Diameter Circle a Semi-Ellipse
Projection of 20 Diameter Circle to Valley Ellipse = 10 ÷ sin 60° = 11.54701 Semi-Major Axis = 11.54701 Semi-Minor Axis = 10 Major Axis = 23.09401 Minor Axis = 20 Equation of Ellipse = 100 x 2 + 133.33333 y 2 = 13333.33333 Projection of 23.09401 × 20 Valley Ellipse width through 30° Plan Angle : 11.54701 × sin 30° = 5.77350 NOTE : The Minor Axis is the Horizontal Dimension on the x-axis; the Major Axis is the Vertical Dimension on the y-axis. Semi-Major Axis = 10 Semi-Minor Axis = 5.77350 Major Axis = 20 Minor Axis = 11.54701 Equation of Ellipse = 100 x 2 + 33.33333 y 2 = 3333.33333 Let the horizontal dimension on the 11.54701 × 20 Ellipse = 4 Height of 11.54701 × 20 Ellipse 2 = ( 3333.33333 – 100 × 4 2 ) ÷ 33.33333 = 52 Height of 11.54701 × 20 Ellipse = 7.21111 The Plan Angles are the same, therefore the corresponding horizontal dimension on the 23.09401 × 20 Valley Ellipse remains as per the previous calculation at 4 ÷ sin 30° = 8 Height of 23.09401 × 20 Valley Ellipse 2 = ( 13333.33333 – 100 × 8 2 ) ÷ 133.33333 = 52 Height of 23.09401 × 20 Valley Ellipse = 7.21111 Corresponding horizontal dimension of the 20 Diameter Circle = 8 × sin 60° = 6.92820 The vertical dimension of the 20 Diameter Circle remains 7.21111 HEIGHTS at CORRESPONDING HORIZONTAL DIMENSIONS are EQUAL |
| The full heights of the circles and ellipses need not be used in the construction of the vault. Any value ( for example, 5 ) may be subtracted from all the vertical dimensions to create a new level reference line. |
Validating the Slopes of the Ellipses
Geometric solution of Slope at any Point on the Ellipse

| The slopes of the ellipses at the Framing Points will be evaluated directly from known values according to the formulae: |
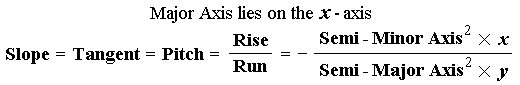
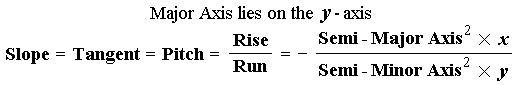
| The slopes will also be tested using the equation: |
|
The slopes to be evaluted have been assigned negative values.
Due to symmetry the slopes in question may actually be positive or negative
(see sketches Solution #1 and Solution #2).
10 Diameter Semi-Circle intercepts 20 Diameter Circle Section: At ( 4 , 3 ) on the 10 Diameter Semi-Circle 10 Diameter Semi-Circle Slope = – ( 5 2 × 4 ) ÷ ( 5 2 × 3 ) = – 4/3 At ( 8 , 3 ) on the 20 × 10 Valley Ellipse 20 × 10 Valley Ellipse Slope = – ( 5 2 × 8 ) ÷ ( 10 2 × 3 ) = – 2/3 Projecting the 10 Diameter Semi-Circle Slope to the 20 × 10 Valley Ellipse: 20 × 10 Valley Ellipse Slope = – 4/3 × sin 30° = – 2/3 At ( 6.92820 , 7.21111 ) on the 20 Diameter Circle 20 Diameter Circle Slope = – ( 10 2 × 6.92820 ) ÷ ( 10 2 × 7.21111 ) = – .96077 Projecting the 20 × 10 Valley Ellipse Slope to the 20 Diameter Circle: – 2/3 ÷ sin 60° = – .76980 ... another inconsistent result Solution #1: Make the 20 Diameter Circle Section a Semi-Ellipse The horizontal dimension on the 17.32051 × 10 Ellipse = 6.92820 At ( 6.92820 , 3 ) on the 17.32051 × 10 Ellipse Slope of 17.32051 × 10 Ellipse = – ( 5 2 × 6.92820 ) ÷ ( 8.66025 2 × 3 ) = – .76980 In accord with the value returned by projecting the Valley Ellipse Slope through the Plan Angle Solution #2: Make the 10 Diameter Circle a Semi-Ellipse At ( 6.92820 , 7.2111 ) on the 20 Diameter Circle 20 Diameter Circle Slope = – ( 10 2 × 6.92820 ) ÷ ( 10 2 × 7.21111 ) = – .96077 Projecting the 20 Diameter Circle Slope to the 23.09401 × 20 Valley Ellipse: 23.09401 × 20 Valley Ellipse Slope = – .96077 × sin 60° = – .83205 At ( 8 , 7.2111 ) on the 23.09401 × 20 Valley Ellipse 23.09401 × 20 Valley Ellipse Slope = – ( 10 2 × 8 ) ÷ ( 11.54701 2 × 7.21111 ) = – .83205 Projecting the 23.09401 × 20 Valley Ellipse Slope to the 11.54701 × 20 Ellipse: 11.54701 × 20 Ellipse Slope = – .83205 ÷ sin 30° = – 1.66410 NOTE : The Minor Axis lies on the x-axis and the Major Axis lies on the y-axis Therefore the Slope = – [ Semi-Major Axis 2 × x ] ÷ [ Semi-Minor Axis 2 × y ] At ( 4 , 7.2111 ) on the 11.54701 × 20 Ellipse 11.54701 × 20 Ellipse Slope = – ( 10 2 × 4 ) ÷ ( 5.77350 2 × 7.21111 ) = – 1.66410 |