|
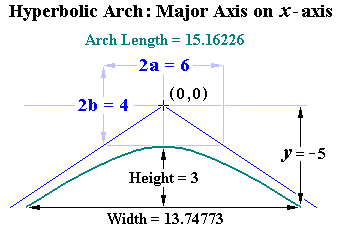
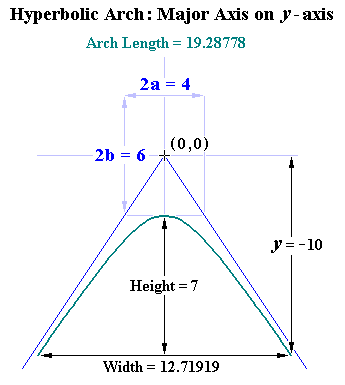
Hyperbolic Axis Calculations
(x/a) ² – (y/b) ² = – 1
Arch Height = h Arch Width = w
Given : Semi-Axis on the y-axis = b
|
The equation of the Ellipse is written as:
b ² x ² – a ² y ² = – a ² b ² , where x = w / 2 and y = b + h Therefore : b ² x ² = a ² y ² – a ² b ² Collecting terms : b ² x ² = a ² ( y ² – b ² ) Dividing both sides of the equation by ( y ² – b ² ) : a ² = b ² x ² / ( y ² – b ² ) Taking the square root of both sides of the equation : a = bx / Ö ( y ² – b ² ) , and the axis on the x-axis = 2a |
Given : Semi-Axis on the x-axis = a
|
The equation of the Ellipse is written as:
b ² x ² – a ² y ² = – a ² b ² , where x = w / 2 and b = y – h Transposing the term from the right side : a ² y ² – b ² x ² – a ² b ² = 0 Collecting like terms : a ² y ² – b ² ( a ² + x ² ) = 0 Dividing by ( a ² + x ² ) : y ² a ² / ( a ² + x ² ) – b ² = 0 Substituting for b to express the equation in terms of y and h : y ² a ² / ( a ² + x ² ) – ( y – h ) ² = 0 Expanding the term ( y – h ) ² : y ² a ² / ( a ² + x ² ) – ( y ² – 2 y h + h ² ) = 0 Removing the parentheses : y ² a ² / ( a ² + x ² ) – y ² + 2 y h – h ² = 0 Collecting terms : y ² [ a ² / ( a ² + x ² ) – 1 ] + y 2 h – h ² = 0 The equation is quadratic in y, where : A = a ² / ( a ² + x ² ) – 1 B = 2 h C = – h ² Substituting in the General Quadratic Equation : [ – B ± Ö ( B ² – 4 A C ) ] / 2A returns the value of y Therefore b = y – h , and the axis on the y-axis = 2b Although only one value for b is returned by the calculator, due to the ± sign in the General Quadratic Equation there are two possible solutions. The calculator returns values based on the negative value of the discriminant. |
Given : Equal Semi-Axes
|
The equation of the Ellipse is written as:
a ² x ² – a ² y ² = – a ² a ² , where x = w / 2 and y = a + h Therefore : a ² = y ² – x ² Substituting for x and y : a ² = ( a + h ) ² – (w / 2 ) ² Expanding the terms : a ² = a ² + 2 a h + h ² – w ² / 4 Transposing terms and multiplying all terms by 4 : 4 a h = w ² – 4 h ² Dividing both sides by 4 h : a = ( w ² – 4 h ² ) / 4 h |