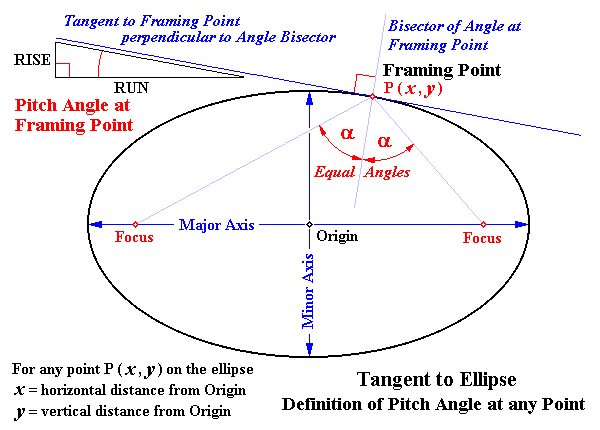
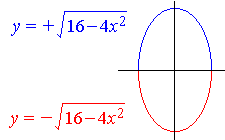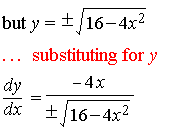Geometric Solution of Slope of Ellipse
Differentiating with respect to the Eccentric Angle
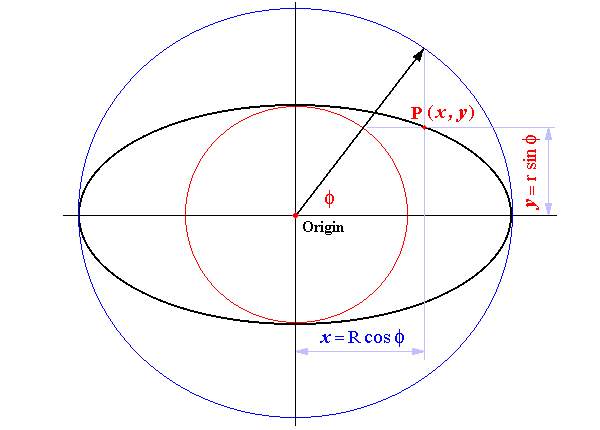
Parametric Equations of an Ellipse
|
R = Semi - Major Axis
r = Semi - Minor Axis Differentiating with respect to f dy/df = d(r · sinf)/df = r · cosf dx/df = d(R · cosf)/df = R · (– sinf) Since cosf = x/R and sinf = y/r Substituting for sinf and cosf dy/df = r · x/R dx/df = R · (– y/r) Slope at any point on the Ellipse = dy/dx dy/dx = (dy/df) / (dx/df) Substituting for dy/df and dx/df dy/dx = (r · x/R) / (– R · y/r) dy/dx = – (r ² · x) / (R ² · y) Since R = Semi - Major Axis and r = Semi - Minor Axis |

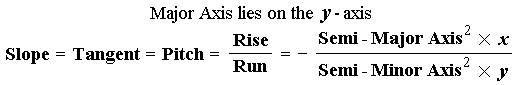
Resolving the ellipse
4x2 + y2 = 16
in terms of y explicitly as a function of x and differentiating with respect to x.
dy/dx = d(16 - 4x2)1/2/dx dy/dx = d(16 - 4x2)1/2/d(16 - 4x2) • d(16 - 4x2)/dx ... Chain Rule 
The solution for the function in the negative y quadrants returns the same terms but with opposite sign.
Using Implicit Differentiation to differentiate
4x2 + y2 = 16
with respect to x
|