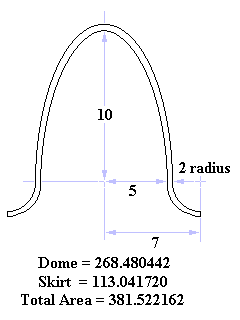
Dome (Ellipsoid) Surface Area Calculation
|
a = 5 b = 10 f1 = 0 f2 = .5π Δf = (.5π – 0)/4 = .125π 1 × 5 cos (0 × .125π) × Ö ((5 sin (0 × .125π)) ² + (10 cos (0 × .125π)) ² = 50 4 × 5 cos (1 × .125π) × Ö ((5 sin (1 × .125π)) ² + (10 cos (1 × .125π)) ² = 174.3 2 × 5 cos (2 × .125π) × Ö ((5 sin (2 × .125π)) ² + (10 cos (2 × .125π)) ² = 55.9 4 × 5 cos (3 × .125π) × Ö ((5 sin (3 × .125π)) ² + (10 cos (3 × .125π)) ² = 45.9 1 × 5 cos (4 × .125π) × Ö ((5 sin (4 × .125π)) ² + (10 cos (4 × .125π)) ² = 0 (π/24) × (50 + 174.3 + 55.9 + 45.9) = 42.7 2π × 42.7 = 268.3 ... Javascript Calculator: 268.480442 |
Skirt (Torus) Surface Area Calculation
|
R = 7 a = 2 b = 2 f1 = π f2 = 1.5π Δf = (1.5π – π)/4 = .125π 1 × ( 7 + 2 cos ( π + 0 × .125π)) × Ö ((2 sin (π + 0 × .125π)) ² + (2 cos (π + 0 × .125π)) ² = 10 4 × ( 7 + 2 cos ( π + 1 × .125π)) × Ö ((2 sin (π + 1 × .125π)) ² + (2 cos (π + 1 × .125π)) ² = 41.2 2 × ( 7 + 2 cos ( π + 2 × .125π)) × Ö ((2 sin (π + 2 × .125π)) ² + (2 cos (π + 2 × .125π)) ² = 22.3 4 × ( 7 + 2 cos ( π + 3 × .125π)) × Ö ((2 sin (π + 3 × .125π)) ² + (2 cos (π + 3 × .125π)) ² = 49.9 1 × ( 7 + 2 cos ( π + 4 × .125π)) × Ö ((2 sin (π + 4 × .125π)) ² + (2 cos (π + 4 × .125π)) ² = 14 (π/24) × (10 + 41.2 + 22.3 + 49.9 + 14) = 18 2π × 18 = 113.1 ... Javascript Calculator: 113.041720 |
Total Surface Area = 268.3 + 113.1 = 381.4