Trigonometric
Formulas and Relationships

Definition of Ratios
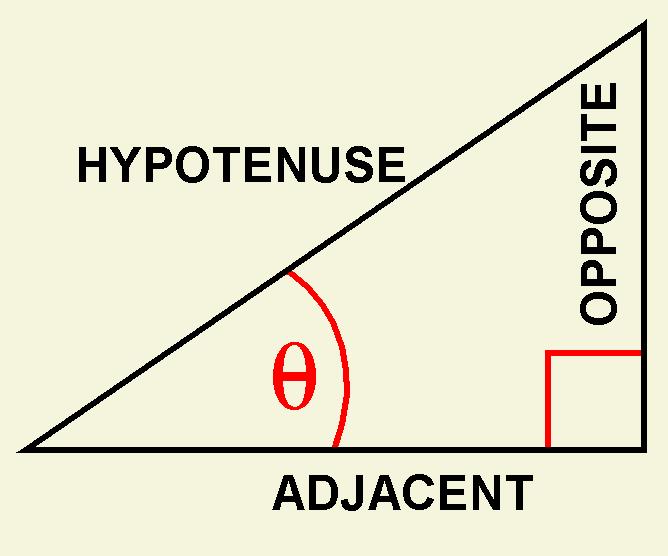
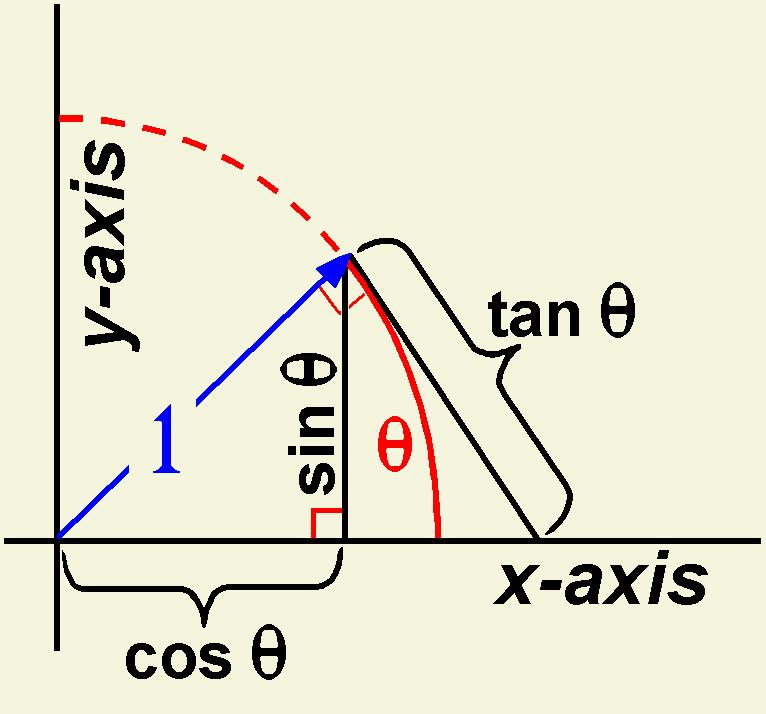
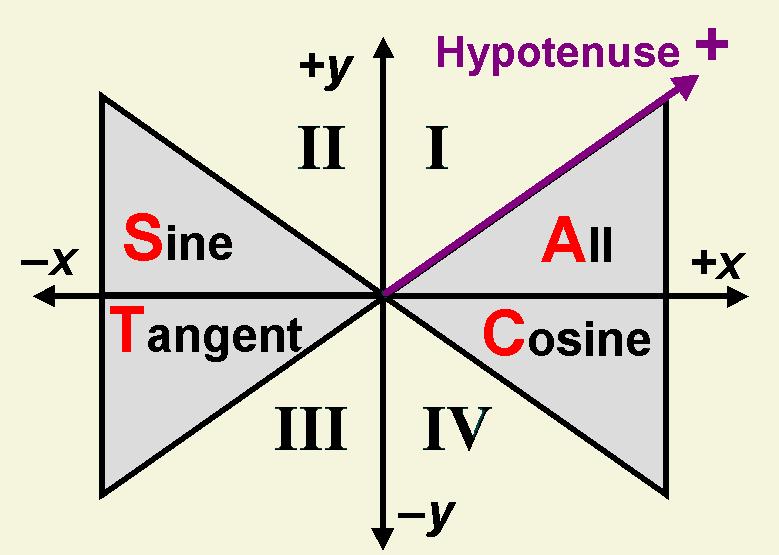
Geometric interpretation of Trig Functions
The sides of the triangle and the trig functions are defined with respect to the location of the angle     Sine = Opposite / Hypotenuse
    Cosine = Adjacent / Hypotenuse
    Tangent = Opposite / Adjacent
    Cosecant = Hypotenuse / Opposite
    Secant = Hypotenuse / Adjacent
    Cotangent = Adjacent / Opposite

Fundamental Identities:
sin x / cos x = tan x
cos x / sin x = cot x = 1 / tan x
sec x = 1 / cos x
csc x = 1 / sin x
sin2 x + cos2 x = 1
tan2 x + 1 = sec2 x = 1 / cos2 x
cot2 x + 1 = csc2 x = 1 / sin2 x

Geometric interpretation of the Fundamental Trigonometric Identities: The symbol theta is substituted for the variable x used in the formulas
Reduction Formulas diagram, showing changes of sign according to quadrant (CAST rule)

Reduction Formulas:
sin (90 - x) = cos x
cos (90 - x) = sin x
tan (90 - x) = 1 / tan x = cot x
More Reduction Formulas


Sum Identities:
sin (a + b) = sin a cos b + sin b cos a
cos (a + b) = cos a cos b - sin b sin a
tan (a + b) = (tan a + tan b) / (1 - tan a tan b)

Difference Identities:
sin (a - b) = sin a cos b - sin b cos a
cos (a - b) = cos a cos b + sin b sin a
tan (a - b) = (tan a - tan b) / (1 + tan a tan b)

Double Angle Relationships:
sin2 x = (1 - cos 2x) / 2
cos2 x = (1 + cos 2x) / 2
sin 2x = 2 sin x cos x
cos 2x = cos2 x - sin2 x = 2 cos2 x - 1 = 1 - 2 sin2 x
tan 2x = 2 tan x / (1 - tan2 x)

Half Angle Relationships:
sin (x/2) = [(1 - cos x) / 2]½
cos (x/2) = [(1 + cos x) / 2]½
tan (x/2) = [(1 - cos x) / (1 + cos x)]½
               = (1 - cos x) / sin x = sin x / (1 + cos x)

Factorization Equations:
sin a + sin b = 2 sin[(a + b)/2] cos[(a - b)/2]
sin a - sin b = 2 cos[(a + b)/2] sin[(a - b)/2]
cos a + cos b = 2 cos[(a + b)/2] cos[(a - b)/2]
cos a - cos b = -2 sin[(a + b)/2] sin[(a - b)/2]

Product Formulas:
sin x sin y = [cos(x - y) - cos(x + y)] / 2
sin x cos y = [sin(x - y) + sin(x + y)] / 2
cos x cos y = [cos(x - y) + cos(x + y)] / 2


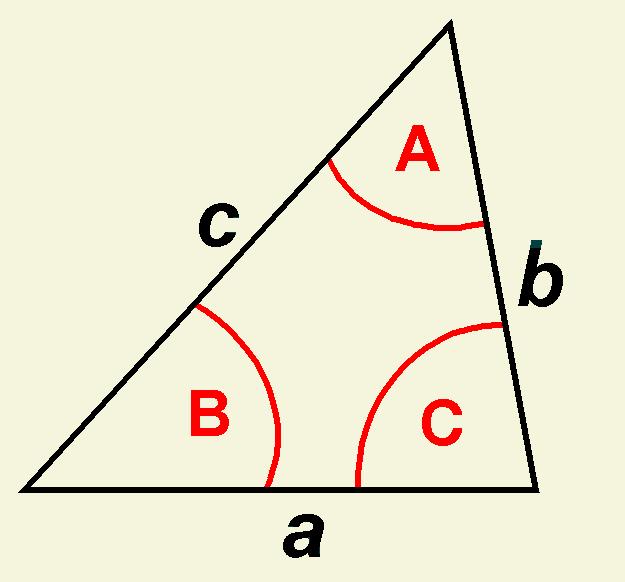
Law of Sines:
a /sin A = b /sin B = c /sin C

Law of Cosines:
a2 = b2 + c2 - 2bc cos A
If A = 90 degrees, then cos 90 = 0,
and the equation reduces to the
Pythagorean Theorem : a2 = b2 + c2 		Diagram showing the side and angle relationships for Law of Sines and Law of Cosines formulas


Pythagorean Triples:
x and y are positive integers, x > y :
Let a = x2 + y2 , b = 2xy , and c = x2 - y2
Then a2 = b2 + c2

a sin x + b cos x:
Let q = arctan (- b / a)
Then a [sin x - (- b cos x / a)]
= a (sin x - tan q cos x )
= a (sin x - sin q cos x / cos q)
= a (sin x cos q - cos x sin q) / cos q
= a sin (x - q) / cos q

HOME PAGE

1