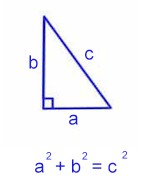
You should always label the hypotenuse as c. The legs, however, can be interchanged. See the picture to the left.
The Pythagorean Theorem
The theorem is named after the Greek
Mathematician, Pythagoras who was one of the first Mathematicians to present a
proof of the statement. There are many proofs of this theorem and many examples
which illustrate this theorem on the internet. If you do an internet search with
the words "Pythagorean Theorem Proof" or just "Pythagorean Theorem", you will
find many articles which will greatly enhance your understanding of the
theorem. You will sometimes see the theorem stated in sentence
form as " the sum of the squares of the legs is equal to the square of the
hypotenuse".
Theorem 6.1 (Pythagorean Theorem)
|
Click for an animated proof of the Pythagorean Theorem. (Close the window when you are finished viewing.)
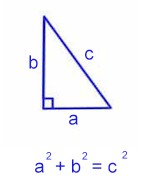
You should always
label the hypotenuse as c. The legs, however, can be interchanged. See
the picture to the left.
The converse of the Pythagorean Theorem is true. The statement of the converse is: Any triangle which satisfies the relationship, a2+ b2 =c2 , is a right triangle.
We will use the Pythagorean Theorem to find unknown sides of
right triangles. We use the converse to determine if a triangle with given sides
is a right triangle.
Example 6.1 Find the length of the hypotenuse of a right triangle with legs of length 4 inches and 9 inches. [Solution]
Example 6.2 Assume one leg of a right triangle is twice as long as the other leg. If the hypotenuse of the triangle is 12 meters, find the lengths of the two legs. [Solution]
Example 6.3 Show that the triangle with sides of length 6 feet, 8 feet and 10 feet is a right triangle. [Solution]
Special Right Triangles
Some right triangles are "special" because the
lengths of the sides are whole numbers. An example is given below. The numbers
(3,4,5), (5,12,13) and (16,30,34) are called Pythagorean Triples. There are infinitely many such triples.
As an exercise, see if you can find other Pythagorean Triples which are not
multiples of (3,4,5) or (5,12,13).
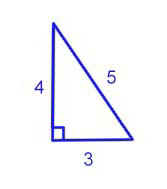
32 + 42 = 52
9 + 16 = 25
25 = 25
Other right triangles are "special" because of their angles. Two
such triangles are the 30-60-90 degree triangle and the 45-90 degree right
triangle. These are pictured below and visual justification for each is provided
by clicking on each picture.
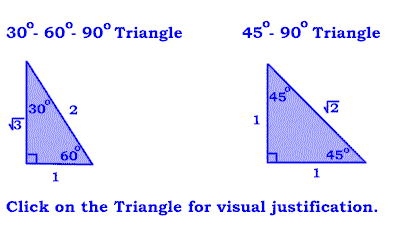
As a general rule, we should memorize these triangles because they will be important when we study similar triangles.