
Physics
World
Back to Electrodynamics
Consider
the two equations for E and B

Substituting
Eq. (1b) into Eq. (1a) to get

Since
the curl of the expression in the bracket vanishes it follows that the quantity
can be written as a scalar, which is chosen here to be -F, i.e.
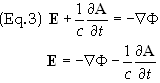
However,
consider the following quantities, A' and F',
defined by the following
transformation
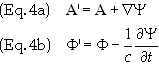
Y(r,
t) is an arbitrary function which has continuous second derivatives of
both space and time variables. Eq.
(4) is referred to as a gauge transformation where Y(r,
t) is referred to as a gauge function. Take the partial derivative
of Eq. (4a) with respect to time and multiply through by 1/c, then take
the gradient of Eq. (4b) to obtain, respectively
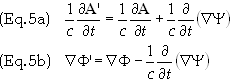
Add Eqs.
(5a) and (5b) together to get
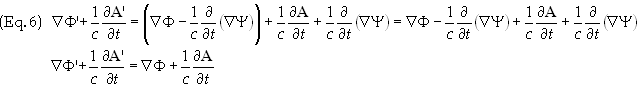
This
demonstrates that E is invariant under a gauge transformation, i.e.
![]()
Therefore
the electric field E can be written in terms of either A and F
or A' and F'
for an arbitrary function Y
whose gradient is well defined. Now substitute Eq. (7) into Eq. (2), use the
identity Ñ´(ÑY) = 0, to get
![]()
Therefore
the transformation defined by Eq. (4) leaves both E and B
unchanged. Such a property is called gauge invariance.
Upon substituting Eq. (3) into Coulomb's Law gives
![]()
or
![]()
Substituting
Eq. (1b), i.e. B
= Ñ´A,
into Ampere's Law gives

Employing
the identity Ñ´(Ñ´A)
= Ñ(Ñ·A)
- Ñ2A
in Eq. (11)
results in
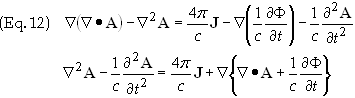
The
potentials, A and F, have a degree of arbitrariness up until this point.
An additional condition can therefore be imposed on them. This can accomplish in
several ways. However there are two conditions that are useful.
Eq. (12) can be uncoupled by imposing the following condition
![]()
This
condition is called the Lorenz condition. If A and F
do not satisfy the Lorenz condition then a gauge transformation can be done and
then demand that the new potentials, A' and F',
satisfy the Lorenz condition. I.e. we demand
![]()
The task
then becomes that of finding new potentials, A' and F',
to satisfy this relation. Thus we substitute Eq. (4) into Eq. (14) to get

If there
exists a gauge function that satisfies Eq. (16) then the new potentials, A'
and F',
will satisfy the Lorenz condition. Therefore the restricted Lorenz condition is

satisfies
the Lorenz condition. Potentials that satisfy Eq. (25) belong to a class of
gauges that are called the Lorenz gauge. Another gauge that is useful is
the so-called Coulomb gauge and is the gauge for which
![]()
Back
to Electrodynamics
Physics World