Helmholtz Theorem
Physics
World
Back to Electrodynamics
If a
vector field F whose divergence Ñ·F
= b(r) and curl Ñ´F =
c(r) are known and entirely contained within a finite region of
space then F is uniquely determined and has the value
![]()
where
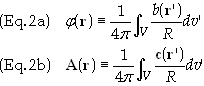
The
variables in Eq. (2) are defined as
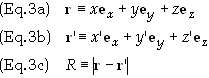
The
prime coordinates represent the source coordinates whereas the unprimed
coordinates represent the field coordinates.
Proof:
It can be shown that
![]()
d
is the Dirac delta function defined by the following properties

Using
Eq. (3) and Eq. (4b) F can be expressed as
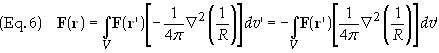
It is
important to remember that Ñ2
is defined in terms of the unprimed coordinates. As such it can be brought
through the integral to the outside to yield

Using
the identity -Ñ2C
= Ñ(Ñ·C)
- Ñ´(Ñ´C)
Eq. (6a) can be written as
![]()
Define f
and A as follows
![]()
In terms
of f and
A we can write Eq. (7) as (see comments in Appendix)
![]()
Ñ
and Ñ’
are defined and related by
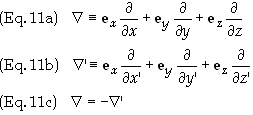
It can
be show that
![]()
To find
f in
terms of b(r’) we substitute Eq. (6b) into the definition of
f (Eq.
(8a) ) to obtain

F
can be brought outside the divergence by using the identity
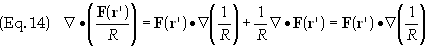
The
relation Ñ·F(r’)
= 0 has been employed in Eq. (13). This follows from the fact that F is a
function only of the primed coordinates whereas the derivatives in the
divergence are with respect to the unprimed coordinates. Eq. (13) is substituted
into Eq. (12) to obtain
![]()
Substitute
the identity in Eq. (13), replacing Ñ
with Ñ’
to obtain
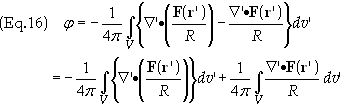
Utilizing
the divergence theorem, and substituting Ñ’·F’(r’)
= b(r’) into Eq. (15) we get
![]()
Since,
by assumption, the source, b, is restricted to a finite region and thus
can be contained entirely contained within a surface S then S and V
can be chosen to be a sphere of radius r which entirely contains the
source within it. The last integral on the right side of Eq. (16) remains
finite. Regarding the first integral on the right; as the radius of the surface
increases as r then the area of the surface increases as r2.
However the integrand decreases as r3.
Therefore as we let the radius go to infinity we see that the first integral
vanishes. Eq. (18) then becomes
![]()
This is
just the relation in Eq. (2a) that we wished to arrive at.
To find A in terms of c(r’) we
follow a very similar procedure to what we have done above. Substitute the
definition of C in Eq. (6b) into the definition of A into Eq. (8b)
to obtain
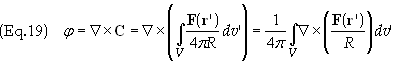
F
can be brought outside the curl by using the identity
![]()
The last
term on the right side of Eq. (19) vanishes, i.e. Ñ´F(r’)
= 0. This follows from the fact that F is entirely a function of the
primed coordinates whereas the derivatives in the curl are with respect to the
unprimed coordinates. Substitute Eq. (19) into Eq. (18) and then employ the
identity in Eq. (11) to obtain
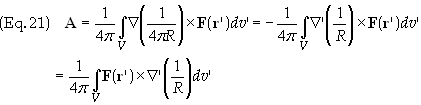
Utilizing
the identity in Eq. (19), replacing Ñ
with Ñ’,
Eq. (20) becomes
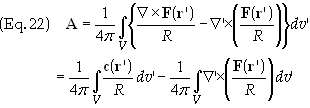
Applying a modified version of Gauss’s theorem Eq. (21) becomes
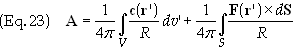
For
reasons similar to those applied to Eq. (16) the first integral vanishes
yielding the final result
![]()
This is
just the relation in Eq. (2b) that we wished to arrive at. This completes the
proof of the Helmholtz theorem.
Uniqueness
theorem
The
solution F
which satisfies Ñ·F
= b(r) and
Ñ´F
= c(r)
is unique if the sources are bounded in space and the fields
vanish at sufficiently large distances from the sources.
Proof:
Suppose there are two functions, F1
and F2,
which satisfies
Ñ·F
= b(r) and Ñ´F
= c(r). I.e.
![]()
Define
the vector W º
F1
- F2>.
It follows from Eq. (24) that
![]()
Since
the curl of W is zero it can be expressed as the gradient of a scalar,
i.e.
![]()
It
follows from Eq. (26) and Eq. (25b) that
![]()
Apply
the divergence theorem to the vector D º
YÑY
gives

Inserting
Eq. (27) reduces Eq. (28) to give
![]()
Let S be
any spherical surface of radius r that encloses all sources. As r
becomes large compared to the dimensions of the sources Y
goes to zero as 1/ r
and ÑY
goes to 1/r2.
Therefore YÑY
goes to zero as 1/r3.
Since the surface increases as r2
it follows that the surface integral on the left hand side goes to zero. Since
the integrand on the right side is always positive it follows that ÑY
= 0 and thus W = 0.
I.e.
![]()
Therefore F as defined in Eq. (1) is unique.
Appendix
It
should be noted that the gradient of an arbitrary continuous function Y
can be added to A and
leave F unchanged. To see this make the substitutions A ®
A + ÑY
![]()