Lorentz Force and Generalized Potential
Physics
World
Back to Electrodynamics
Vectorial
Approach
The
Lorentz force on a charged particle moving in an electromagnetic field is given
by
![]()
Substituting
the values of the electric and magnetic fields in terms of the Coulomb and
vector potential, respectively, i.e.

the
Lorentz force becomes
![]()
Recall
the vector identity
![]()
Letting a
= v and b = A we obtain
![]()
The
terms including spatial derivatives of the velocity are zero which leaves
![]()
Solving
for v´(Ń´A)
gives
![]()
Substitute
this expression into Eq. (3)
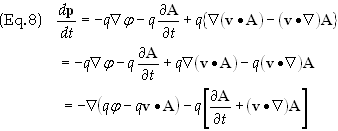
The
first term on the right hand side is an example of what is known as a generalized
potential and usually labeled U, i.e.
![]()
The
second term is the convective derivative of A whose value is the
total derivative of A, i.e.
![]()
Substituting
the expressions in Eqs. (9) and (10) into Eq. (8) we obtain
![]()
Eq. (12)
can be rearranged to give
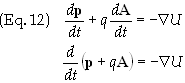
The canonical
or generalized 3-momentum, P, for a charged particle in an EM
field has the value
![]()
Therefore
in terms of P and U the Lorentz force in Eq. (1) can be written as
![]()
The time
rate of change of the canonical momentum is called the canonical 3-force
and will here be labeled F. Thus Eq. (1) now takes on the simple form
![]()
Analytical Approach
The
result obtained above in Eq. (15) can more readily be obtained using Lagrangian
mechanics. Start with the Lagrangian for a charged particle in an
electromagnetic field
![]()
If we
define the following quantities
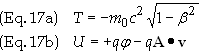
Then the
Lagrangian can be expressed in a more familiar form
![]()
The canonical
momentum of a particle, p,
is defined in terms of the Lagrangian as
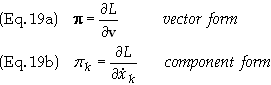
Inserting
these into Lagrange’s equations
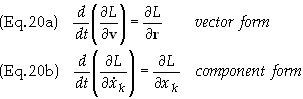
we get
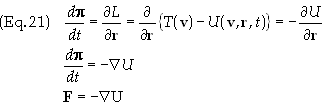
F
is the canonical force defined as the time rate of change of the
canonical momentum. It can readily be shown that p has the value
![]()
The
result in Eq. (21) is identical to the result obtained above in Eq. (15).
Back
to Electrodynamics
Physics World