-
Symbol Defintion
Example GT means greater than
Q01. Diagram of pedal triangle
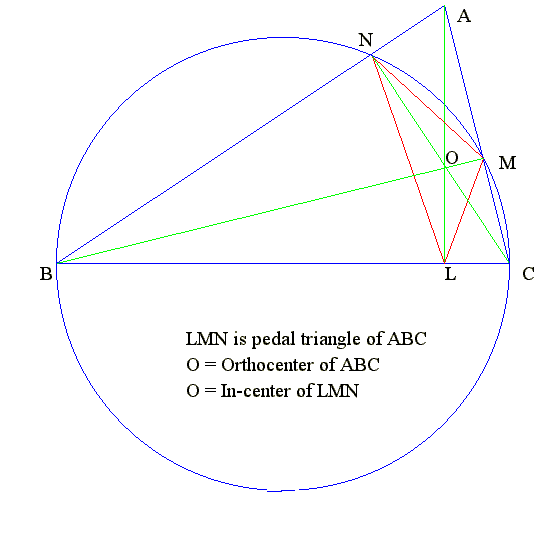
- Orthocenter
- AL, BM and CN are altitudes of triangle ABC.
- AL, BM and CN meet at one point O is called orthcenter.
- Joint the feet of AL, BM and CN give triangle LMN.
- Trinagle LMN is called pedal triangle.
- Properties
- Orthocenter O is also the in-center of triangle LMN.
- Then AL is bisector of MLN.
- Then BM is bisector of LMN.
- Then CN is bisector of MNL.
Go to Begin
Q02. Prove that AL is bisector of angle MLN
Geometric Method
- Draw circle using BC as diameter then BNMC is conclic.
- Angle BNM + angle ANM = 180. Straight angle.
- Angle BNM + Angle ACB = 180. Conclic.
- Hence angle ANM = angle ACB.
- Draw circle using AC as diameter then ANLC is conclic.
- Angle BNL + angle ANL = 180. Straight angle.
- Angle ANL + Angle ACL = 180. Conclic.
- Hence angle BNL = angle ACL = angle ACB.
- Hence angle ANM = angle BNL.
- Since angle BNC = angle ANC = 90 degrees.
- Hence angle LNC = angle MNC and CN is bisector of angle LNM.
- Similarly, AL is bisector of angle MCN and BM is bisector of angle LMN.
- Hence O is also the incenter of triangle LMN.
- Give coordinates of vertex A, B and C.
- Let AL, BM and CN are the altitudes of triangle ABC.
- Find coordinates of L using intersections of BC and AL.
- Find equation of BC using two given points.
- Find equation of AL using point and slope method.
- Slope of BC is s = (YB-YC)/(XB-XC) and slope of AL is -1/s.
- Solve above two equations and we have (XL,YL).
- Find coordinates of M using intersections of AC and BM.
- Find coordinates of N using intersections of AB and CN.
- Find angle ALN.
- Find slope of NL as s1.
- Find slope of AL as s2.
- Then tan(ALN) = (s1 - s2)/(1 + s1*s2).
- Find angle ALM.
- Find slope of ML as s3.
- Find slope of AL as s2.
- Then tan(ALN) = (s2 - s3)/(1 + s2*s3).
- Hence we have angle ALN = angle ALM.
- Hence AL is bisector of angle MLN.
- Similary, BM is bisector of angle LMN and CN is bisector of MNL.
- Hence O is the in-center of triangle LMN.
- Draw triangle ABC.
- Draw AL perpendicular to BC.
- Draw BM perpendicular to CA.
- Draw CN perpendicular to AB.
- Joint L, M and N which is the pedal triangle LMN of triangle ABC.
- Measure angle ALN and angle ALM.
- We should have angle ALN = angle ALM.
- Hence AL is bisector of angle MLN.
- Similary, BM is bisector of angle LMN and CN is bisector of MNL.
- Hence O is the in-center of triangle LMN.
Go to Begin
Q03. Prove that A is the es-center of triangle LMN
Geometric method
- Produce LN to P and Prove that Angle PNA = angle ANM.
- Angle ANC = 90 degrees.
- Angle ANM = Angle ANC - Angle MNC = 90 - angle MNC.
- Angle PNM = angle NLM + angle NML = 180 - MNL.
- Angle MNL = 2*(angle MNC).
- Angle PNM = 180 - angle MNL.
- Angle PNA = angle PNM - angle ANM
- Angle PNA = (180 - MNL) - (90 - MNL/2) = 90 - MNL/2 = angle ANM
- Hence NA is bisector of angle PNM
- Produce LM to Q and Prove that Angle QMA = angle NMA.
- Same as above, we can prove that MA is the bisectior of angle QMA.
- Hence A is the es-center of triangle LMN.
Contruction method
- Produce LN to P and LM to Q
- Measure angle ANP and ANM. We should have angle ANP = angle ANM.
- Hence NA is bisector of angle PNM.
- Similarly, MA is bisector of angle QMN
- AL is bisector of MLN.
- Hence A is the es-center of triangle LMN. Study subject Five centers of a triangle.
Go to Begin
Q04. Pedal trinagle and ex-central triangle
- Triangle LMN is the pedal triangle of triangle ABC.
- Triangle ABC is the ex-central triangle LMN.
- Proof : See Q02 or Q03.
Go to Begin
Q05. Find angles of pedal triangle LMN in terms of angles A, B and C
The relations
- Angle MLN = 180 - 2*(angle A).
- Angle LMN = 180 - 2*(angle B).
- Angle MNL = 180 - 2*(angle C).
- From Q02, we have angle ANM = angle C and angle BNL = angle C.
- Angle MNL = 180 - angle ANM - angle BNL = 180 - (angle C)
- Similarly, we can prove the other two identities.
Go to Begin
Q06. Sides of pedal triangle
Construction
- Draw a triangle ABC
- AD is perpendicular to BC and D is on BC
- BE is perpendicular to BC and E is on CA
- CF is perpendicular to CA and F is on AB
- Trinagle DEF is pedal triangle of triangle ABC
- DE = AB*cos(C) = c*cos(C)
- In triangle ADE, using sine law
- DE/sin(EAD) = AD/sin(AED)
- DE = (AD*sin(EAD))/sin(AED)
- In right angle triangle ADB, AD = AB*sin(B)
- DE = (AB*sin(B)*sin(EAD))/sin(AED)
- Use AB as diameter draw a circle, then A, B, D, E are concycli
- Then angle B = pi - angle AED and sin(AED) = sin(B)
- Hence DE = AB*sin(EAD)
- In right triangle ADC, angle EAD = angle CAD = 90 - C. sin(EAD) = cos(C)
- Hence DE/ = c*cos(C)
- Similarly EF = a*cos(A)
- Similarly FD = b*cos(B)
Go to Begin
Q07. Area of pedal triangle
- Area of triangle DEF
- = ((EF)*(FD)*sin(DFE))/2
- = (a*cos(A))*(b*cos(B))*(sin(180 - 2*C))/2
- = (2*R*sin(A)*cos(A))*(2*R*sin(B)*cos(B))*sin(2*C))/2
- = (R^2)*sin(2*A)*sin(2*B)*sin(2*C))/2
- Where R is the circum-radius of triangle ABC
- The proof is based on sine law
- a = 2*R*sin(A)
- b = 2*R*sin(B)
- c = 2*R*sin(C)
Go to Begin
Q08. Circum-radius of pedal triangle
- Circum-radius of pedal triangle
- = EF/(2*sin(EDF))
- = (R*sin(2*A))/(2*sin(180 - 2*A)
- = R/2
- a = 2*R*sin(A)
- b = 2*R*sin(B)
- c = 2*R*sin(C)
Go to Begin
Q09. Answer
Go to Begin
Q10. Answer
Go to Begin
