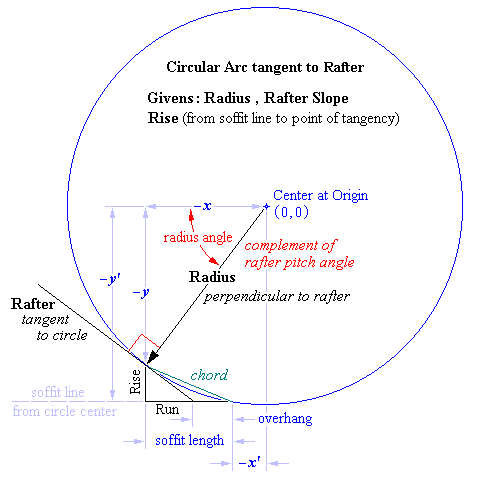
Circular Arc tangent to Rafter Foot: Excel Worksheet
Models and Drawings of an Irregular Ski Slope Roof
|
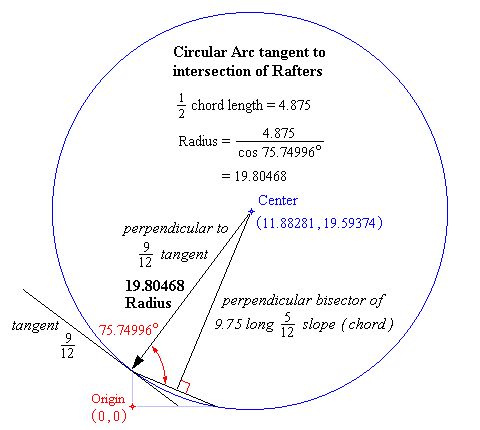
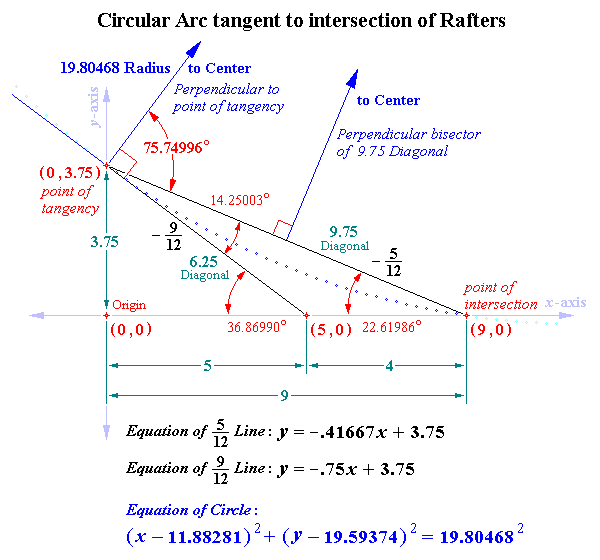
5/12 Pitch Angle = 22.61986°
9/12 Pitch Angle = 36.86990° 12/9 (radius) Pitch Angle: 90° – 36.86990° = 53.13010° Working Angle: 22.61986° + 53.13010° = 75.74996° Chord (5/12 slope) length = 9.75 ½ chord length = 4.875 Radius of circle: 4.875/cos 75.74996° = 19.80468 |
Solutions given the Radius of the Circle
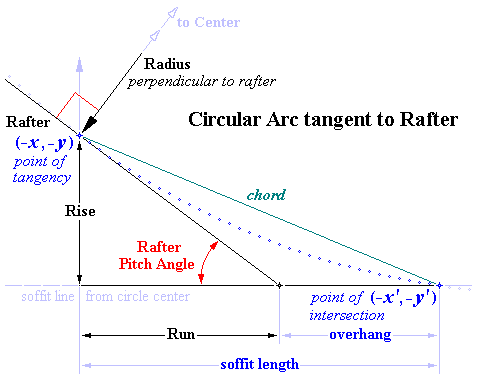
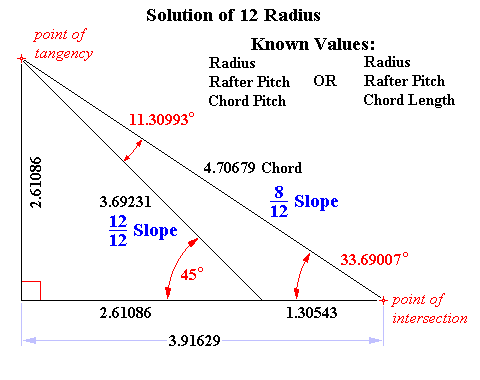
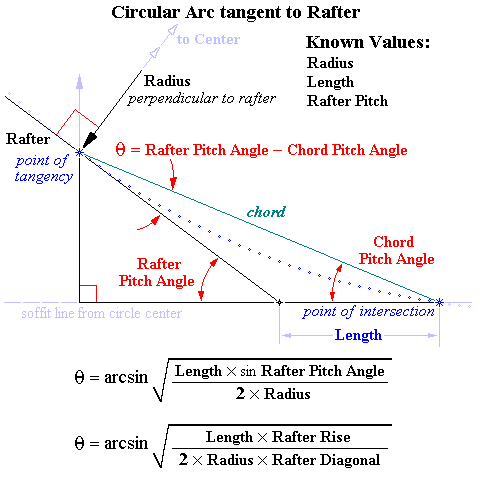
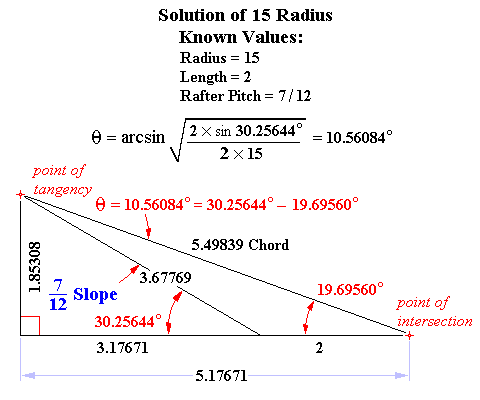
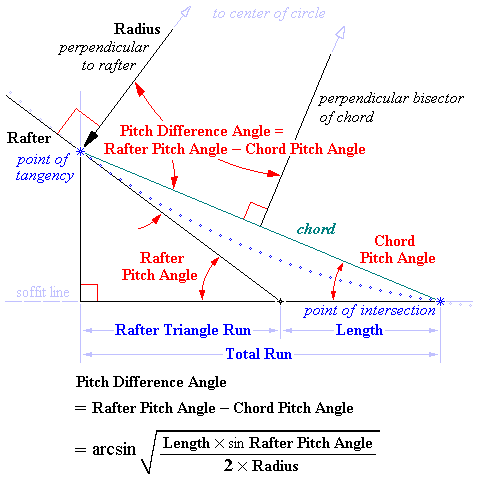
Solution of ( Rafter Pitch Angle – Chord Pitch Angle ) Formula
|
Rafter Pitch Angle = RPA°
Chord Pitch Angle = CPA° Pitch Difference Angle = Rafter Pitch Angle – Chord Pitch Angle = PDA° Length = Total Run – Rafter Triangle Run Triangle of the Rafter Diagonal, Chord and Chord Pitch Angle ... Law of Sines Chord / sin (180° – RPA°) = Length / sin PDA° Since sin (180° – RPA°) = sin RPA° ... Chord / sin RPA° = Length / sin PDA° Chord = Length × sin RPA° / sin PDA° ... Chord Equation 1 Formula for the Radius ... Radius = ½ Chord / cos (90° – RPA° + CPA°) ½ Chord = Radius × cos (90° – RPA° + CPA°) Working with respect to the complementary central angle ... ½ Chord = Radius × sin PDA° Chord = 2 × Radius × sin PDA° ... Chord Equation 2 Chord Equation 1 = Chord Equation 2 ... Length × sin RPA° / sin PDA° = 2 × Radius × sin PDA° Length × sin RPA° / (2 × Radius) = sin PDA° × sin PDA° sin PDA° = Square Root (Length × sin RPA° / (2 × Radius)) PDA° = arcsin (Square Root (Length × sin RPA° / (2 × Radius))) |