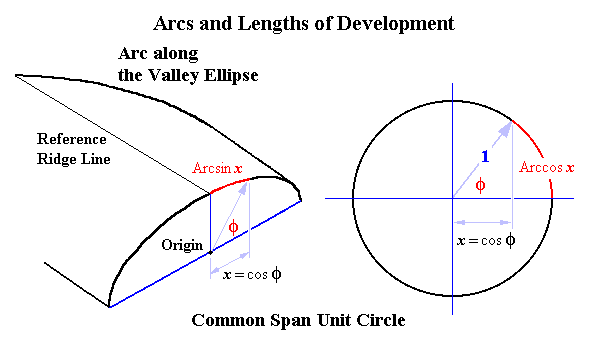
| The lengths shown in the sketches are multiplied by the radius of the circle to determine the dimensions for an actual development. |
|
For any station x,
equal to the length to be measured from the adjoining ridge line in plan,
the corresponding dimension developed on the work is Arcsin x,
producing the curve:
y = Arcsin x |
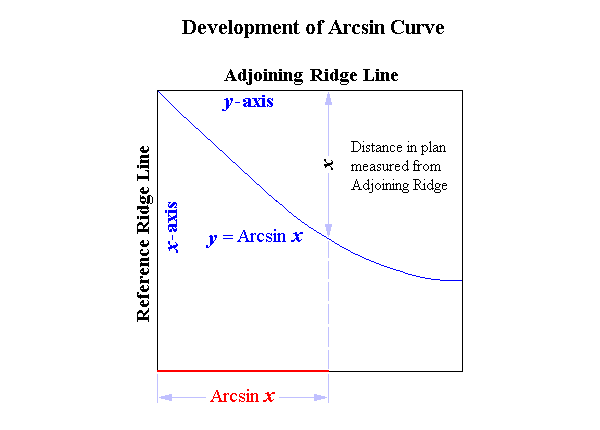
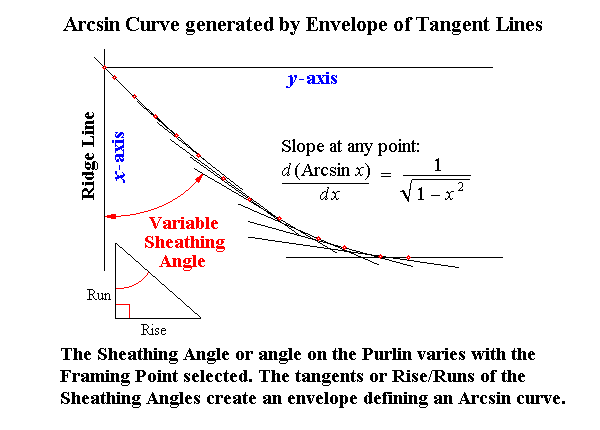
| DEVELOPMENT of ARCSIN CURVE: SAMPLE DATA |
| x from Center | Tangent to Circle | Sheathing Angle | Sheathing Angle Slope |
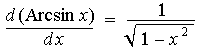
|
| 1.00000 | Undefined | 90.00000° | Undefined | Undefined |
| .99000 | 7.01792 | 81.97041° | 7.08880 | 7.08881 |
| .95000 | 3.04243 | 72.65901° | 3.20256 | 3.20256 |
| .90000 | 2.06474 | 66.44809° | 2.29416 | 2.29416 |
| .80000 | 1.33333 | 59.03620° | 1.66667 | 1.66667 |
| .70000 | .98020 | 54.46780° | 1.40028 | 1.40028 |
| .60000 | .75000 | 51.34019° | 1.25000 | 1.25000 |
| .50000 | .57735 | 49.10660° | 1.15470 | 1.15470 |
| .40000 | .43644 | 47.49432° | 1.09109 | 1.09109 |
| .30000 | .31449 | 46.35044° | 1.04829 | 1.04828 |
| .20000 | .20412 | 45.58467° | 1.02062 | 1.02062 |
| .10000 | .10050 | 45.14395° | 1.00504 | 1.00504 |
| Zero | Zero | 45.00000° | 1.00000 | 1.00000 |
Solving and Checking the Arc Lengths
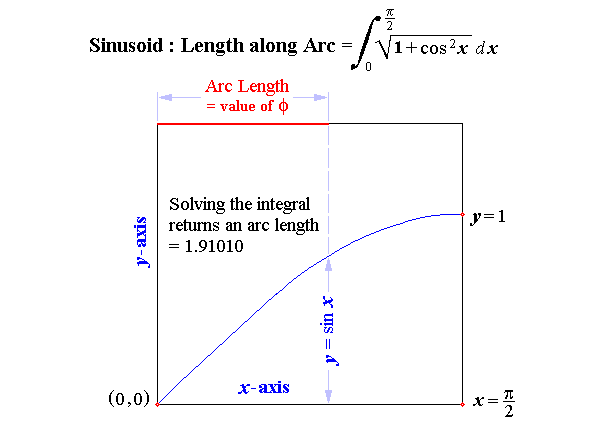
| The arc length of the developed curve equals the arc length of the ellipse. Transposing the co-ordinates about the axes of the graph of the arcsin curve results in the graph of the sinusoid below. |
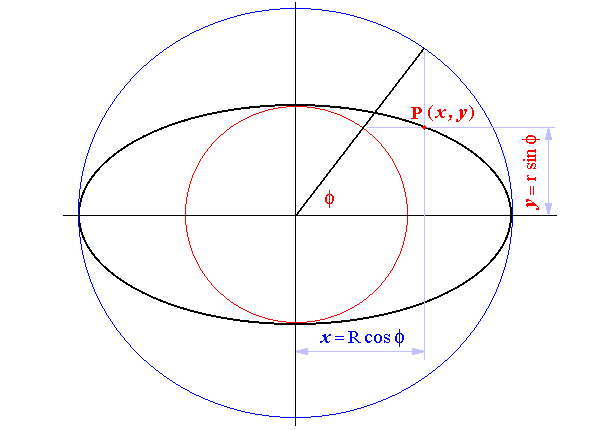
The ellipse may be defined in terms of a Parametric Angle, φ.
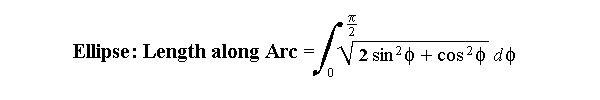
Integrating from zero to π/2 with respect to φ returns an arc length of 1.91010.
Back to Main Page