|
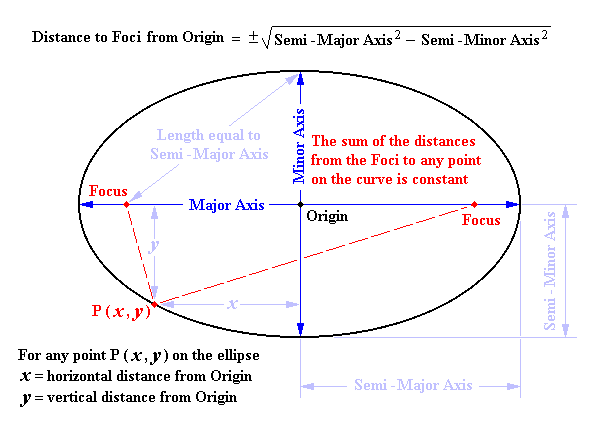
PROJECTION of DIMENSIONS on the x-axis:
The Deck Angle is the Angle viewed in Plan between the Ridge and Valley Run.
RISES (y) are equal for all corresponding RUNS (x)
Valley Run = Main Run ÷ sin Deck Angle
= Main Run ÷ sin 53.13010°
Valley Run = Adjacent Run ÷ sin Deck Angle
= Adjacent Run ÷ sin 36.86990°
Example:
Valley Run = 9.33333 ÷ sin 53.13010° = 11.66667
PURLIN LENGTH and DIFFERENCE in LENGTH:
Starting at the ridge or centerline, each successive Purlin shortens in length by the distance between them as viewed in plan divided by the tangent of the Deck Angle.
Example:
The distance from the ridge to the first Purlin and each successive Purlin seen in plan is 16"
Purlin Difference in Length = 16" ÷ tan 53.13010° = 12"
Beginning at the ridge, each Purlin is 12" shorter than its neighbor.
Find the length of the Purlin at 9.33333 from the ridge or centerline.
Purlin Length = 9.33333 ÷ tan 53.13010° = 6.99999
The Purlin in question is 7 units shorter than the ridge.
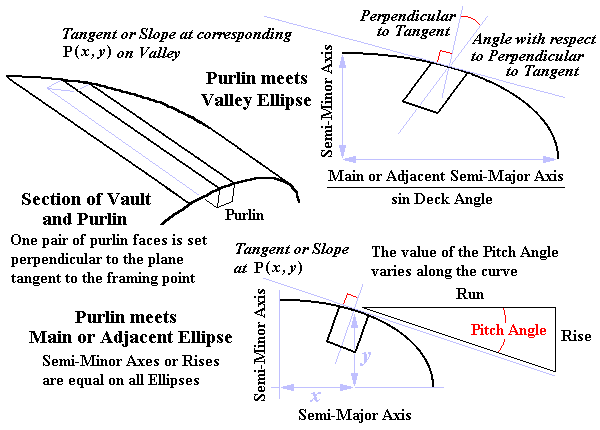
SLOPE at any POINT on the CURVE:
At corresponding points the Valley slope conforms to the standard Hip-Valley Pitch Formula.
Valley Slope = Main Slope × sin Deck Angle
= Main Slope × sin 53.13010°
Valley Slope = Adjacent Slope × sin Deck Angle
= Adjacent Slope × sin 36.86990°
Example:
Valley Slope = - 1.29986 × sin 53.13010° = - 1.03989
The Tangent to a point on the ellipse defines the Slope, Pitch or Rise ÷ Run.
The Slopes along the curves of the ellipses are constantly changing.
Slope at any point = - (Semi-Minor Axis ² × x) ÷ (Semi-Major Axis ² × y)
Example:
At (x, y) = (9.33333, 1.79506) on the MAIN SPAN
Slope = - (5 ² × 9.33333) ÷ (10 ² × 1.79506) = - 1.29986
At (x, y) = (11.66667, 1.79506) on the VALLEY
Slope = - (5 ² × 11.66667) ÷ (12.5 ² × 1.79506) = - 1.03989
Differentiating the parametric equations of the ellipse with respect to the Parametric Angle φ
returns the following formula for the slope at any point:
Slope = - Semi-Minor Axis ÷ ( Semi-Major Axis × tan φ)
Example: Given the parametric equations x = 10 cos φ and y = 5 sin φ
dx/dφ = d(10 cos φ)/dφ = -10 sin φ
dy/dφ = d(5 sin φ)/dφ = 5 cos φ
Slope = dy/dx = 5 cos φ / -10 sin φ = -1 ÷ 2 tan φ
For any point (x, y) on the ellipse the Parametric Angle φ may be determined by the either of the following formulas:
φ = arccos(x ÷ Semi-Major Axis)
φ = arcsin(y ÷ Semi-Minor Axis)
At (x, y) = (9.33333, 1.79506) on the MAIN SPAN
φ = arccos(9.33333 ÷ 10) = .36721
φ = arcsin(1.79506 ÷ 5) = .36721
tan φ = .38466 and substituting in the formula for the slope returns:
Slope = -1 ÷ 2 tan φ = -1 ÷ (2 × .38466) = - 1.29986
|
|
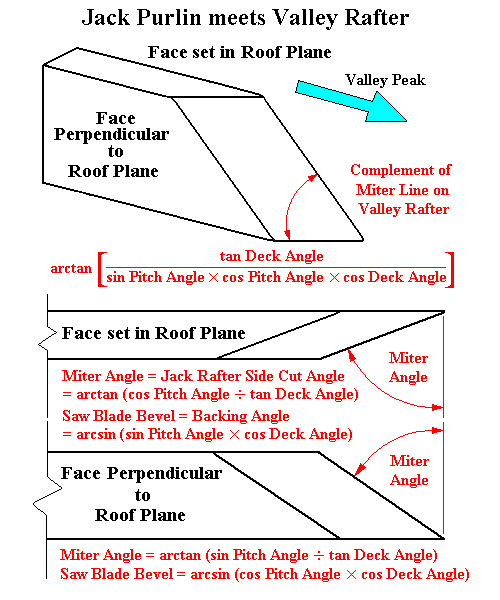
PURLIN MITER and BEVEL ANGLE FORMULAS:
GIVEN: Slope at the Framing Point and Deck Angle
Pitch Angle in the following formulas means arctan(Slope at the Framing Point)
Plane of the Roof means the plane tangent to the curve at the framing point.
The compound angle is cut on the face of the Purlin set perpendicular to the plane of the roof.
Saw Miter = arctan(sin Pitch Angle ÷ tan Deck Angle)
Angle on the Stick = arctan(tan Deck Angle ÷ sin Pitch Angle)
or Angle on the Stick = 90° - Saw Miter
Saw Blade Bevel = arcsin(cos Pitch Angle × cos Deck Angle)
Miter Line on the Valley: In the context of an ellipse, the following angle
is measured with respect to a right angle to the tangent (meaning Slope or Pitch) at a given point.
arctan(sin Pitch Angle × cos Pitch Angle × cos Deck Angle ÷ tan Deck Angle)
Example:
At (x, y) = (9.33333, 1.79506) on the MAIN SPAN,
the Slope = 1.29987
(Invoking symmetry, we may use a positive value of the slope)
Pitch Angle = arctan(1.29987) = 52.42864°
Saw Miter = arctan(sin 52.42864° ÷ tan 53.13010°) = 30.72919°
Angle on the Stick = arctan(tan 53.13010° ÷ sin 52.42864°) = 59.27081°
or Angle on the Stick = 90° - 30.72919° = 59.27081°
Saw Blade Bevel = arcsin(cos 52.42864° × cos 53.13010°) = 21.45987°
Corresponding point (x, y) = (9.33333, 1.79506) on the VALLEY
, Slope = 1.03989
With respect to a right angle drawn to this line the Purlin meets the Valley at
arctan(sin 52.42864° × cos 52.42864° × cos 53.13010° ÷ tan 53.13010°)
= 12.26950°
The compound angle is cut on the face of the Purlin set in the plane of the roof
Saw Miter = Jack Rafter Side Cut Angle = arctan(cos Pitch Angle ÷ tan Deck Angle)
Angle on the Stick = Sheathing Angle = arctan(tan Deck Angle ÷ cos Pitch Angle)
or Angle on the Stick = 90° - Saw Miter = 90° - Jack Rafter Side Cut Angle
Saw Blade Bevel = Backing Angle = arcsin(sin Pitch Angle × cos Deck Angle)
Example:
Saw Miter = arctan(cos 52.42864° ÷ tan 53.13010°) = 24.57518°
Angle on the Stick = arctan(tan 53.13010° ÷ cos 52.42864°) = 65.42482°
or Angle on the Stick = 90° - 24.57518° = 65.42482°
Saw Blade Bevel = arcsin(sin 52.42864° × cos 53.13010°) = 28.39561°
SPECIAL CASES: The shapes in section may be circular, elliptic, parabolic, hyperbolic, etc.,
or sections thereof.
"Eaves" or "Ridges" may intercept at angles other than 90°.
Equal shapes intercepting at right angles create equal 45° Deck Angles.
The simplest case is two circular sections intercepting at 90°.
Equation: x ² + y ² = Radius ²
Slope at Framing Point = - x ÷ y
Pitch Angle at Framing Point = arctan(x ÷ y)
sin Pitch Angle = x ÷ Radius
cos Pitch Angle = y ÷ Radius
Valley Ellipse Major Axis = Diameter ÷ sin 45°
= Ö2 × Diameter
Example:
Circle: Radius = 5
Framing Point on Circle: at x = 4 y = 3
Slope at Framing Point = tan Pitch Angle = - 4 ÷ 3
Pitch Angle = arctan (4 ÷ 3) = 53.13010°
sin Pitch Angle = 4 ÷ 5 cos Pitch Angle = 3 ÷ 5
Valley Ellipse Major Axis
= 5 × Ö2
= 7.07107
Corresponding Framing Point on Valley Ellipse:
x = 4 × Ö2 = 5.65685 y = 3
Since tan 45° = 1 and sin 45° = cos 45° = 1 ÷
Ö2
some Deck Angle terms in the Purlin formulas are eliminated and the equations reduce to simpler forms.
Angles on the Purlin face perpendicular to the plane of the roof:
Saw Miter = arctan(sin Pitch Angle)
Angle on the Stick = arctan(1 ÷ sin Pitch Angle)
= arctan(csc Pitch Angle)
Saw Blade Bevel = arcsin(cos Pitch Angle ÷
Ö2)
@
arcsin(.70711 × cos Pitch Angle)
Example:
Saw Miter = arctan(4 ÷ 5) = 38.65981°
Angle on the Stick = arctan(5 ÷ 4) = 51.34019°
Saw Blade Bevel = arcsin(3 ÷ (5 ×
Ö2))
= 25.10409°
Angles on the Purlin face set in the plane of the roof:
Saw Miter = arctan(cos Pitch Angle)
Angle on the Stick = arctan(1 ÷ cos Pitch Angle)
= arctan(sec Pitch Angle)
Saw Blade Bevel = arcsin(sin Pitch Angle ÷
Ö2)
@
arcsin(.70711 × sin Pitch Angle)
Example:
Saw Miter = arctan(3 ÷ 5) = 30.96376°
Angle on the Stick = arctan(5 ÷ 3) = 59.03624°
Saw Blade Bevel = arcsin(4 ÷ (5 ×
Ö2))
= 34.44990°
Miter Line on the Valley =
arctan(sin Pitch Angle × cos Pitch Angle ÷
Ö2)
@
arctan(.70711 × sin Pitch Angle × cos Pitch Angle)
Example:
Miter Line on the Valley =
arctan(4 × 3 ÷ (5 × 5 ×
Ö2))
= 18.74779°
|