-
Symbol Defintion
Sqr(x) = Square root of x
Q01. Study the curve of y = 1/(2*x)
Properties of the curve
- 1. It is symmetrical to line y = x
- 2. It has asymptotes x = 0 and y = 0
- 3. It is a function
- 4. The signs of y
- If x LT 0, y is negative (Curve is in 4th quadrant)
- If x GT 0, y is positive (Curve is in 1st quadrant)
- 5. Signs of y' = -1/(2*x^2)
- If x LT 0, y' is negative (Curve is decreasing)
- If x GT 0, y' is negative (Curve is decreasing)
- 6. Signs of y' = -1/(x^3)
- If x LT 0, y" is negative (Curve is concave downward)
- If x GT 0, y' is positive (Curve is concave upward)
- If the curve is rotate 45 degrees, the equation is
- 1/(x^2) - 1/(y^2) = +1. It is hyperbola with principal axis y = 0
- 1/(x^2) - 1/(y^2) = -1. It is hyperbola with principal axis x = 0
- Since y = 1/(2*x) is hyperbola with principal axis y = x
- Hence the curve y = 1/(2*x) is symmetrical to line y = +x (its own inverse)
- Hence the curve y = 1/(2*x) is symmetrical to line y = -x
- Rotation reference : See AN 14
- If A(1, 1/2) is a point on curve
- Then B(1/2, 1) is also a point on inverse
- Hence points A and B are on curve y = 1/(2*x)
- Slope of AB = (1 - 1/2)/((1/2) - 1) = -1
- Hence AB is perpendicular to the line y = x
- Mid point AB is xm = (1 + 1/2)/2 = 0.75 and ym = (1/2 + 1)/2 = 0.75
- Hence the mid point of AB is on line y = x
- Hence A and B are symmetrical to the line y = x
-
Grphic calculator
Program 03 08
- Load the program
- Click start to get menu
- Click 03 in upper box
- Click 08 in lower box
- Give data for y = 1/(2*x) : 0, 0, 0, 1, 0, 0, 2, 0
Go to Begin
Q02. Study the graph of R = 1 + 1*sin(11*A/4)^3
Diagram in application program
-
Patterns
Program 21 10
- Load the program
- Click menu
- Click 10 in upper box
- Click 01 in lower box
- Give data for R = a + b*sin(p*A/q)^M : 1, 1, 11, 4, 3
-
Patterns
p = 11, q = 4 and M = 3
-
Patterns
Program 05 04
- Load the program
- Click start to get menu
- Click 05 in upper box
- Click q = 4 in lower box
- 1. Cycle domain is 0 to 4*q*(2*pi)
- 2. Maximum value of R = a + b = 2
- 3. It is 11 small petals and 11 large petals
Go to Begin
Q03. Convert (x/5)^2 + (y/3)^2 = 1 to polar form
Diagrams Diagram on internet
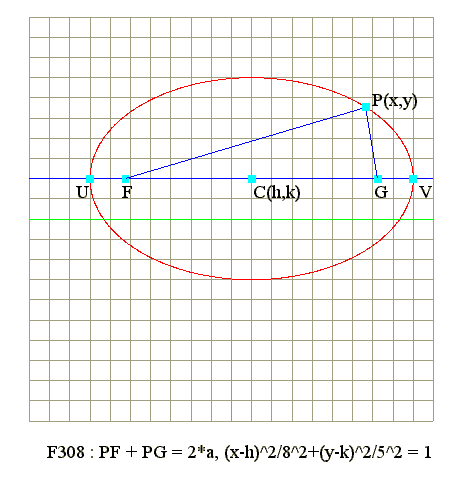
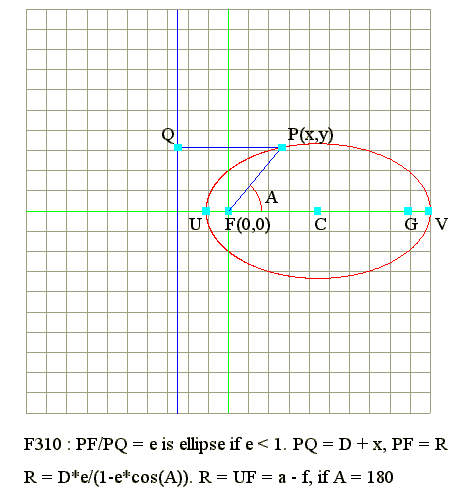
- Defintion
- Given a = 5 and b = 3
- Hence f = Sqr(a^2 - b^2) = Sqr(5^2 - 3^2) = 4
- e = f/a = 4/5 = 0.8
- Find D : From above two diagram, we can see that
- In rectangular form : UF = CU - CF = a - f
- In polar form : R is corresponding to UF when A = 180
- Since cos(180) = -1
- Hence R = (D*e)/(1 + e) = UF = a - f
- Hence D*e = (a - f)*(1 + e)
- Hence D = (5 - 4)*(1 + 0.8)/0.8 = 2.25
- The polar form is R = (2.25*0.8)/(1 - 0.8*cos(A))
- R = 1.8/(1 - 0.8*cos(A))
- Since origin is at F in polar form
- Hence we translate equation as ((x - 4)/5)^2 + (y/3)^2 = 1
- Change equation as 9*(x - 4)^2 + 25*y^2 = 9*25
- Simplify 9*x^2 - 9*8*x + 9*16 + 25*y^2 = 9*25
- Since R^2 = x^2 + y^2 and y = R*sin(A)
- 9*x^2 + 25*y^2 = 9*(x^2 + y^2) + 16*y^2
- = 9*R^2 + 16*(R^2)*sin(A)^2
- Hence 9*R^2 + 16*(R^2)*sin(A)^2 - 72*R*cos(A) = 9*(25 - 16)
- Hence 9*(1 + (16/9)*sin(A)^2) - 72*R*cos(A) = 9*9
- Hence (R^2)*(1 + (16/9)*sin(A)^2) - 8*R*cos(A) = 9
- Since cos(A)^2 + sin(A)^2 = 1
- Hence (R^2)*(1 + 16/9 - (16/9)*cos(A)^2) - 8*R*cos(A) = 9
- Hence (25/9)*(R^2) = (16/9)*(R*cos(A))^2 + 8*R*cos(A) + 9
- Hence (25/9)*(R^2) = (4*R*cos(A)/3 + 3)^2
- Square root both sides
- 5*R/3 = 4*R*cos(A)/3 + 3
- 5*R = 4*R*cos(A) + 9
- 5*R - 4*R*cos(A) + 9
- R = (9/5)/(1 - 0.8*cos(A))
- R = 1.8/(1 - 0.8*cos(A))
-
Analytic geometry
AN 07 00
Go to Begin
Q04. Convert R = 1.8/(1 - 0.8*cos(A)) to rectangular form
Diagrams Diagram on internet


- Find D and e
- from the equation we see that e = 0.8
- D*e = 1.8 and D = 2.25
- Find a and b
- In rectangular form : UF = CU - CF = a - f
- In polar form : R is corresponding to UF when A = 180
- Since cos(180) = -1
- Hence R = (D*e)/(1 + e) = UF = a - f
- Hence D*e = (a - f)*(1 + e)
- Hence 1.8 = (a - f)*(1 + 0.8) or a - f = 1
- Since f/a = e
- Hence a - a*e = 1
- a = 1/(1 -e) = 5 and f = 4
- b^2 = a^2 - f^2 = 25 - 16 = 9 or b = 3
- Hence the equation is (x/5)^2 + (y/4)^2 = 1
- R = 1.8/(1 - 0.8*cos(A))
- R*(1 - 0.8*cos(A)) = 1.8
- Since x = R*cos(A), hence R - 0.8*x = 1.8 or R = 1.8 + 0.8*x
- Square both sides : R^2 = (1.8 + 0.8*x)^2
- Since R^2 = x^2 + y^2, hence x^2 + y^2 = 1.8^2 + 2*1.8*0.8*x + 0.64*x^2
- Simplify : 0.36*x^2 - 2.88*x + y^2 = 3.64
- o.36*(x^2 -4*x + 16 - 16) + y^2 = 3.64
- Completing square 0.36*(x - 4)^2 + y^2 = 9
- Divide by 9 on both sides : (0.36/9)*(x - 4)^2 + y^2/9 = 1
- Hence ((x - 4)/5)^2 + (y/3)^2 = 1
-
Analytic geometry
AN 07 00
Go to Begin
Q05. Find equation of directrix of (x/5)^2 + (y/4)^2 = 1
Solution : Related with focus F
- Find D : From Q03, we know D = 2
- Find f : From Q03, we know f = 4
- Find coordinate of F : xf = 0 - f = -4 and yf = 0
- Hence equation of directrix is x = xf - D = -6
- Find D : From Q03, we know D = 2
- Find f : From Q03, we know f = 4
- Find coordinate of G : xf = 0 + f = 4 and yf = 0
- Hence equation of directrix is x = xf + D = 6
Go to Begin
Q06. Sketch y = x + 1/x
Diagram on internet
-
Graphic of ratioanl functions
y = x + 1/x
- 1. Find asymptotes
- x = 0 and y = infinite, hence x = 0 is vertical asymptote
- x = infinite and y = x, hence y = x is line asymptote
- Sketch lines : x = 0 and y = x
- 2. Find signs of y when x LT 0
- x LE -1, y from -infinite to -2 (Increasing)
- 0 LT 0 and x GE -1, y from -2 to -infinite at x = 0 (decreasing)
- The curve is between x = 0 and y = x
- The curve is in 3rd quadrant
- 3. Find signs of y when x GT 0
- 0 GT x and LE 1, y from +infinite to +2 (decreasing)
- x GE 1, y from 2 to +infinite (increasing)
- The curve is between x = 0 and y = x
- The curve is in 1st quadrant
- 4. Extreme points at (-1,-2) and (1,2)
- 1. Find y' and y"
- y = x + 1/x
- y' = 1 - 1/(x^2)
- y" = +2/x^3
- 2. Draw asymptotes as method 1
- 3. x LT -1
- y' GT 0 and y is increasing from -infinite to -2
- y" LT 0 and curve is concave downward
- 3. -1 GT x and x LT 0
- y' LT 0 and y is decreasing from -2 to -infinite
- y" LT 0 and curve is concave downward
- 4. x GT 0 and x LT 1
- y' LT 0 and y is decreasing from +infinite to 2
- y" GT 0 and curve is concave upward
- 5. x LG 1
- y' GT 0 and y is increasing from 2 to +infinite
- y" GT 0 and curve is concave upward
- 6. Extreme points at (-1,-2) and (1,2)
-
Graphic of ratioanl functions
Section 03 48 : y = x + 1/x
Go to Begin
Q07. Sketch y = x^2 + 1/x
Diagram on internet
-
Graphic of ratioanl functions
y = x + 1/x
- 1. Find asymptotes
- x = 0 and y = infinite, hence x = 0 is vertical asymptote
- x = infinite and y = x^2, hence y = x^2 is parabola asymptote
- Sketch lines x = 0 and parabola y = x^2
- 2. Find signs of y when x LT 0
- x LE -1, y = 0 and y from +infinite to 0 (decreasing)
- 0 LT 0 and x GE -1, y from 0 to -infinite at x = 0 (decreasing)
- The curve is at left side of x = 0
- The curve is concave upward if x LT -1 and downward if x between -1 and 0
- The curve is inside y = x^2 when x LT -5
- 3. Find signs of y when x GT 0
- x GT 0, y from +infinite go to minimum and then go +infinte
- The curve is between x = 0 and y = x^2 when x is large
- The curve is decreasing and concave upward between x = 0 and minimumu point
- The curve is increasing and concave upward when x GT minimumu point
- 1. Find y' and y"
- y = x^2 + 1/x
- y' = 2*x - 1/(x^2)
- y" = 2 + 2/(x^3)
- 2. Draw asymptotes as method 1
- 3. x LT -1
- y' LT 0 and y is decreasing from -infinite to 0
- y" GT 0 and curve is concave upward
- y" EQ 0 if x = -1
- 3. -1 GT x and x LT 0
- y' LT 0 and y is decreasing from 0 to -infinite
- y" LT 0 and curve is concave downward
- 4. x GT 0 and x LT minimum point
- y' LT 0 and y is decreasing from +infinite to minimum
- y" GT 0 and curve is concave upward
- 5. x LG 1
- y' GT 0 and y is increasing from minimum to +infinite
- y" GT 0 and curve is concave upward
- 6. Point of inflecion at (-1,0) and minimum at ?
-
Grphic calculator
Section 03 08 : rational function
- Method
- Open the program and enter GC
- Click Start and get menu
- Select 03 in upper box
- Select 08 in lower box
- Give coefficient : 1, 0, 0, 1, 0, 0, 1, 0
- Method
-
Grphic of ratioanl functions
Section 03 49 : y = x^2 + 1/x
Go to Begin
Q08. Properties of ((x-2)/5)^2 + ((y+3)/3)^2 = 1
Solutions
- 1. It is an ellipse same as (x/5)^2 + (y/3)^2 = 1
- 2. The principal axis is y = -3
- 3. The center is at (2,-3)
- 4. Semi-axese are a = 5 and b = 3
- 5. Focal length f = Sqr(a^2 - b^2) = 4
- 6. Eccentricity e = f/a = 0.8
- 7. Foci are at F(-2,-3) and G(6,-3)
- 8. Directrix to focus F is 2 (AN 27 05)
- 9. Equivalent polar form is R = 1.6/(1 - 0.8*cos(A)) in AN 27 03
- 10 Distance of point P on curve is PF + PQ = 10
- Describe properties of ((x-2)/3)^2 + ((y+3)/5)^2 = 1
Go to Begin
Q09. Answer
Go to Begin
Q10. Answer
Go to Begin
