Counter
Mathematics Dictionary
Dr. K. G. Shih
Exponent
Subjects

    Read Symbol defintion

  • Q01 | - Defintions of e^x
  • Q02 | - Why do we need exponent ?
  • Q03 | - Why do we use expression e^x ranther than 2^x or 3^x ?
  • Q04 | - Laws of Expenonts
  • Q05 | - Properties of y = e^x
  • Q06 | - The exponential family founctions
  • Q07 | - Euler function e^(ix) = cos(x) + i*sin(x)
  • Q08 | - Inverse of y = e^x
  • Q09 | - Example : e^x + e^(2*x) + e^y + e^(2*y) = 12
  • Q10 | - Solve e^(2*x) + 3*e^x - 18 = 0
  • Q11 | - Example : How sketch e^x + e^(2*x) + e^y + e^(2*y) = 12 ?
  • Q12 | - Example : e^x + e^(2*x) + e^y + e^(2*y) = 12, find y if x = ln(2)
  • Q13 | - Example : Prove that (5^(n+1) + 5^(2*n))/(5 + 5^n) = 5^n
  • Q14 | - Example : Solve 8^(2*x+1) = 4^(5-x)
  • Q15 | - Example : Solve e^x + e^(2*x) < 12
  • Q16 | - The exponential family functions
Answers


Q01. Defintions
  • Symbol : e^x means e to power x.
  • Symbol : EXP(x) means e to power x.
  • Symbol : e^1 = 1 + 1 + 1/2! + 1/3! + 1/4! + 1/5! + ....
  • Symbol : e^x = 1 + x + x^2/2! + x^3/3! + x^4/4! + x^5/5! + ....
  • Note : Change expressions into mathematical forms used in classroom.
Go to Begin

Q02. Why do we need exponent ?
  • Exponent makes mathematical expression simple to read.
  • Example : 2 multiply 2 one hundred times can be expressed as 2^100.
    • 2 multiply 2 one hundred times which need write hundred 2 and hundred x.
    • 2^100 is clearly shown hundred 2 and we do not to count them.
    • It is easier to read and simple to write.
    • This is an example to show that mathematics will make method simple and easy.
  • Example : Who did first use exponent ?
    • Exponential notation was introduced into math field by
    • French scientis Rene Descartes in 17th centrury.
Go to Begin

Q03. Why do we use expression e^x ranther than 2^x or 3^x ?
The expression e^x has the following properties.
  • Expression y = e^x has slope = 1 when x = 0.
  • Derivative of e^x is remaining as e^x.
  • Diferentiation of e^x is also equal to e^x.
  • y = e^(-x) is symmetrical to y = e^x about the y-axis.
Go to Begin

Q04. Laws of exponet
  • 1. Multiplication : (a^x)*(a^y) = a^(x+y).
  • 2. Division : (a^x)/(a^y) = a^(x-y).
  • 3. Poser of power : (a^x)^m = a^(m*x).
  • 4. Power of product : (a*b)^m = (a^m)*(b^m).
  • 5. Power of quotient : (a/b)^m = (a^m)/(b^m).
Special exponent
  • 1. (a^1) = a.
  • 2. Zero exponent : (a^0) = 1.
  • 3. Negative exponent : a^(-n) = 1/(a^n).
  • 4. Rational exponent : a^(1/n) = nth radical of a.
Go to Begin

Q05. Properties of y = e^x
  • 1. y-intercept is at y = 1.
  • 2. The slope is always positive and the curve is always inctreasing.
  • 3. It has asymptote y = 0 and it has no negative value.
  • 4. The curve is always concave upward.
  • 5. y' = e^x and y" = e^x.
  • 6. The series of e^x = Sum[(x^n)/n!] for n from 0 to infinite.
Sketch diagram : quick fee hand sketch
  • x = -1, y = e^x = 0.368
  • x = +0, y = e^x = 1
  • x = +1, y = e^x = 2.718
Go to Begin

Q06. The exponential family founctions
  • Study subject Hyperbolic functions.
  • Functions.
    • sinh(x) = (e^x - e^(-x)/2.
    • cosh(x) = (e^x + e^(-x)/2.
    • tanh(x) = sinh(x)/cosh(x).
    • csch(x) = 1/sinh(x).
    • coth(x) = 1/tanh(x).
    • sech(x) = 1/cosh(x).
Go to Begin

Q07. Euler function e^(ix) = cos(x) + i*sin(x)

 Study subject Complex numbers.
  • Series
    • e^x = 1 + x + x^2/2! + x^3/3! + ....
    • cos(x) = 1 - x^2/2! + x^4/4! - .....
    • sin(x) = x - x^3/3! + x^5/5! - .....
  • e^(ix) = 1 + (ix)^2/2! + (ix)^4/4! + .... + (ix) + (ix)^3/3! + (ix)^5/5! ....
  • e^(ix) = (1 - x^2/2! + x^4/4! + ....) + i*(x - x^3/3! + x^5/5! ....)
  • Hence e^(ix) = cos(x) + i*sin(x).
  • Example : e(i*pi) = cos(pi) + i*sin(pi) = -1.
  • Example : e^(i*pi) = -1 includes most significant symbols -, 1, e, i and pi
Go to Begin

Q08. Inverse of y = e^x
 Go to Begin

Q09. Example : e^x + e^(2*x) + e^y + e^(2*y) = 12
Question
  • Find the equation of tangent to the curve
  • e^x + e^(2*x) + e^y + e^(2*y) = 12
  • when x = ln(3).
Solution
  • Find dy/dx.
    • e^x + 2*e^(2*x) + (e^y)*y' + 2*e^(2*y)*y' = 0.
    • Hence y' = -(e^x + 2*e^(2*y))/(e^y + 2*e^(2*y)).
  • Find e^(2*x) + e^x at x = ln(3)
    • e^x + e^(2*x) = e^x + (e^x)^2.
    • Since e^x = e^ln(3) = 3 (Formula).
    • e^x + e^(2*x) = 3 + 3^2 = 12.
  • Find e^(2*y) + e^y at x = ln(3)
    • e^x + e^(2*x) + e^y + e^(2*y) = 12.
    • Hence 12 + e^y + e^(2*y) = 12
    • Hence e^y + e^(2*y) = 0
  • Find slope at x = ln(3).
    • y' = -(12)/(0) = - infinite
    • Hence equation of tangent at x = ln(3) is a vertical line.
    • Hence equation of tangent is x = ln(3).
    • When x = ln(3), e^y + e^(2*y) = 12 - e^x -e^(2*x) = 12 - 3 - 9 = 0
    • Hence e^y + (e^y)^2 = 0.
    • Or (e^y)*(1 + e^y) = 0.
    • Or e^y = 0 and e^y = -1. Hence e^y = 0 and y = -infinite.
    • Hence x = ln(3) is the asymptote.
Go to Begin

Q10. Solve e^(2*x) + 3*e^x - 18 = 0

  • e^(2*x) = (e^x)^2.
  • Let e^x = u and we have u^2 + 3*x - 18 = 0.
  • Solve quadratic equation : (u - 3)*(u + 6) = 0.
  • Hence u = 3 or u = -6.
  • Since u = e^x is greater than zero, hence the solution is u = 3.
  • Hence e^x = 3 or x = ln(3).

Go to Begin

Q11. Example : How to sketch e^x + e^(2*x) + e^y + e^(2*y) = 12 ?
  • e^(2*y) = (e^y)^2
  • Hence (e^2)^2 + e^y + e^x + e^(2*x)- 12 = 0.
  • Use quadratic formula.
  • Hence e^y = (-1 + Sqr(1^2 - 4*1*(e^x + e^(2*x) - 12)))/(2*1).
  • Take logarithm on both sides
  • Hence y = ln(-1 + Sqr(1^2 - 4*(e^x + e^(2*x) - 12))/2)
Find y
  • Since for ln(u) and u > 0.
  • Hence -1 + Sqr(1 - 4*(e^x + e^(2*x) - 12) > 0.
  • Or Sqr(1 - 4*(e^x + e^(2*x) - 12) > 1.
  • For Sqr(t) and t > 0.
  • Hence (1 - 4*(e^x + e^(2*x) - 12)) > 0.
  • Or (e^x + 2^(2*x) - 12) < 0.
  • Or (e^x)^2 + e^x - 12 < 0.
  • Or (e^x)^2 + e^x - 12 < 0
  • Hence e^x <= (-1 + Sqr(1 + 4*1*12))/2 and e^x > 0.
  • Hence x is between 0 and ln((-1 + Sqr(49))/2).
  • Or x is between 0 and ln(3)
Special points : use e^(ln(t)) = t
  • x = ln(1) = 0
  • y = ln((-1 + Sqr(1 - 4*(1 + 1 - 12))/2) = ln((-1 + Sqr(41))/2).
  • x = ln(2) = 0.6931
  • y = ln((-1 + Sqr(1 - 4*(2 + 4 - 12))/2) = ln((-1 + Sqr(25))/2) = ln(2).
  • x = ln(3) = 1.0986
  • y = ln((-1 + Sqr(1 - 4*(3 + 9 - 12))/2) = ln(0) = -infinite.
diagram

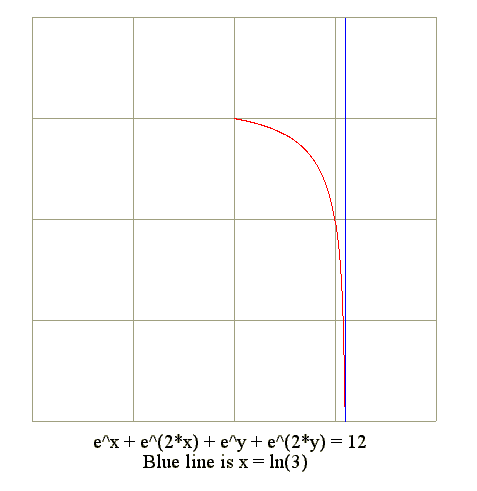
Go to Begin

Q12. e^x + e^(2*x) + e^y + e^(2*y) = 12. Find y if x = ln(2).
  • e^(2*y) = (e^y)^2.
  • Hence (e^2)^2 + e^y + e^(ln(2) + (e^(ln(2))^2 = 12.
  • Use formula e^(ln(t)) = t.
  • Hence (e^y)^2 + e^y + 2 + 2^2 = 12.
  • Hence (e^y)^2 + e^y - 6 = 0.
  • Hence (e^y - 2)*(e^y + 3) = 0
  • since e^y > 0, hence e^y = 2.
  • Hence y = ln(2).

Go to Begin

Q13. Prove that (5^(n+1) + 5^(2*n))/(5 + 5^n) = 5^n
  • 5^(n+1) = 5*5^n and 5^(2*n) = (5^n)^2
  • (5^(n+1) + 5^(2*n)) = 5*5^n + (5^n)^2 = (5^n)*(5 + 5^n).
  • Hence (5^(n+1) + 5^(2*n))/(5 + 5^n) = 5^n.

Go to Begin

Q14. Solve 8^(2*x+1) = 4^(5-x)
Method 1
  • Since 8 = 2^3, hence 8^(2*x+1) = 2^(3*(2*x+1)
  • Since 4 = 2^2, hence 4^(5-x) = 2^(2*(5-x)
  • 2^(3*(2*x+1) = 2^(2*(5-x))
  • Hence 3*(2*x+1) = 2*(5-x)
  • Hence Hence x = 7/8
Method 2
  • Take logarithm on both sides and use log(m^n) = n*log(m)
  • Hence (2*x+1)*log(8) = (5-x)*log(4)
  • Log(8) = log(2^3) = 3*log(2)
  • Log(4) = log(2^2) = 2*log(2)
  • Hence 3*(2*x+1) = 2*(5-x)
  • Hence Hence x = 7/8
Verify
  • x = 7/8 and 8^(2*x+1) = 2^(3*(2*7/8+1) = 2^(66/8) = 2^(33/4)
  • x = 7/8 and 4^(5-x) = 2^(2*(5-7/8)) = 2^(33/4)

Go to Begin

Q15. Solve e^(x) + e^(2*x) < 12
  • Since e^(2*x) = (e^x)^2.
  • Hence (e^x)^2 + e^x - 12 < 0.
  • Or (e^x - 3)*(e^x + 4) < 0.
  • Since e^x is positvie for real x .
  • Hence e^x + 4 greater than 0, hence e^x - 3 is negative.
  • Hence e^x is less than 3.
  • Hence x is greater than ln(1) and less than ln(3)

Go to Begin

Q16. The exponential family functions
Hyperbolic functions
  • sinh(x) = (e^x - e^x)/2.
  • cosh(x) = (e^x + e^x)/2.
  • tanh(x) = sinh(x)/cosh(x)
  • csch(x) = 1/sinh(x)
  • sech(x) = 1/cosh(x)
  • coth(x) = 1/tanh(x)
Reference
Go to Begin
Show Room of MD2002 Contact Dr. Shih Math Examples Room
Copyright © Dr. K. G. Shih, Nova Scotia, Canada.
Hosted by www.Geocities.ws

1