-
Q01 |
- Diagram : Locus of Ellipse
- Q02 | - Defintion of locus of an ellipse
- Q03 | - Equation of locus : (x/a)^2 + (y/b)^2 = 1
- Q04 | - Equation of locus in polar form
- Q05 | - Example : Find equation of locus
- Q06 | - Reference
- Q02 | - Defintion of locus of an ellipse
Q01. Diagram : Locus of an ellipse
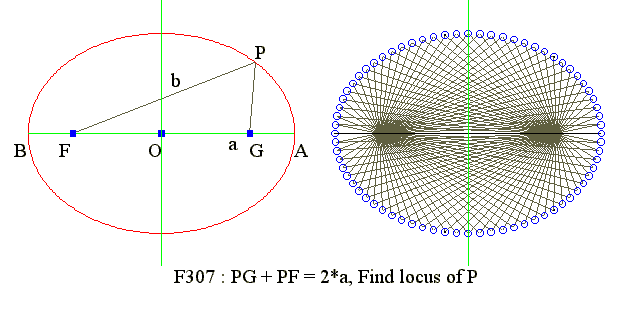
|
Go to Begin
Q02. Defintion of locus of an ellipse
Question
- Point P to fixed points F and G keeping PF + PG = 2*a
- Find locus of point P
- Where F and G are foci and a is the major semi-axis
- The locus is an ellipse
- The equation is (x/a)^2 + (y/b)^2 = 1
Go to Begin
Q03. Equation of locus : (x/a)^2 + (y/b)^2 = 1
Equation
- Let point P(x, y) on ellipse
- Let a, b be semi-axese
- Verteices at U(-a, 0) and V(a, 0)
- Let focal lenth f = Sqr(a^2 - b^2)
- Let F at (-f, 0) and G at (+f, 0)
- By defintion, PF + PG = 2*a
- PF^2 = (x + f)^2 + y^2
- PG^2 = (x - f)^2 + y^2
- Sqr((x + f)^2 + y^2) + Sqr((x - f)^2 + y^2) = 2*a
- Sqr((x + f)^2 + y^2) = 2*a - Sqr((x - f)^2 + y^2)
- Square both sides
- (x + f)^2 + y^2 = (2*a - Sqr((x - f)^2 + y^2))^2
- Simplify
- (x + f)^2 + y^2 = 4*a^2 - 4*a*Sqr((x - f)^2 + y^2) + (x - f)^2 + y^2
- (x + f)^2 - (x - f)^2 - 4*a^2 = 4*a*Sqr((x - f)^2 + y^2)
- 4*x*f - 4*a^2 = 4*a*Sqr((x - f)^2 + y^2)
- (x*f - a^2) = a*Sqr((x - f)^2 + y^2)
- Square both side again
- (x^2)*(f^2) - 2*x*f*(a^2) + a^4 = (a^2)*((x - f)^2 + y^2)
- (x^2)*(f^2) - 2*x*f*(a^2) + a^4 = (a^2)*(x^2 - 2*x*f + f^2 + y^2)
- (x^2)*(f^2) + a^4 = (a^2)*(x^2) + (a^2)*(f^2) + (a^2)*(y^2)
- (x^2)*(a^2 - b^2) + a^4 = (a^2)*(x^2) + (a^2)*(a^2 - b^2) + (a^2)*(y^2)
- -(x^2)*(b^2) = (a^2)*(b^2) + (a^2)*(y^2)
- (x/a)^2 + (y/b)^2 = 1
- General form ((x-h)/a)^2 + (y-k)/b)^2 = 1
- Center is (h, k)
- Vertex is U(h-a, k) and V(h+a, k)
- Focus is F(h-f, k) and G(h+f, k)
- 1. Write the equation of ellipse if center at (-2,3)
- 2. Find coordinates of foci
- 3. Write the equation in parametric form
- 4. Give the equation in polar form
Go to Begin
Q04. Ellipse in Polar form
Polar form
- 1. R = (D*e)/(1 - D*e*cos(A))
- 2. R = (D*e)/(1 + D*e*cos(A))
- 3. R = (D*e)/(1 - D*e*sin(A))
- 4. R = (D*e)/(1 + D*e*sin(A))
- Semi-axese are a and b
- Focal lenth is f
- Ecentricity e = f/a is less than 1
- D is the distance from one focu to the directrix
- Focus to vertex for R = (D*e)/(1 - D*e*cos(A))
- Angle A = 180
- R = distance from focus to vertex
- Hence a - f = (D*e)/(1 + D*e). This is used to find D
Go to Begin
Q05. Find equation of locus
Question
- Two fixed point are F(-4,0) and G(4,0)
- A moving point is P(x,y)
- If PF + PG = 10, find the equation of the motion
- The motion is an ellipse and foci are on the x-axis.
- The equation is (x-h)^2/a^2 + (y-k)^2/b^2 = 1.
- The center C is between F and G. Hence h = 0 and k = 0.
- Also f = CG = CF = 4.
- Since PF + PG = 2*a = 10 by defintion, Hence a = 5.
- Since focal f = Sqr(a^2 - b^2), hence b^2 = a^2 - f^2. and b = 3.
- The requred equation is (x/5)^2 + (y/3)^2 = 1.
- Since PF + PG = 10.
- Sqr((x + 4)^2 + y^2) + Sqr((x - 4)^2+ y^2) = 10
- Sqr((x + 4)^2 + y^2) = 10 - Sqr((x - 4)^2+ y^2)
- Square both sides we have
- (x + 4)^2 + y^2 = (10 - Sqr((x - 4)^2 + y^2))
- (x + 4)^2 + y^2 = 100 - 20*Sqr((x - 4)^2+ y^2)) + (x - 4)^2 + y^2
- (x + 4)^2 - (x - 4)^2 - 100 = -20*Sqr((x - 4)^2+ y^2))
- -16*x + 100 = 20*Sqr((x - 4)^2 + y^2))
- -4*x + 25 = 5*Sqr((x - 4)^2 + y^2))
- Square both sides
- (-4*x + 25)^2 = 25*(x - 4)^2 + 25*Y^2
- 16*x^2 - 200*x + 625 = 25*x^2 - 200*x + 400 - 25*y^2
- -9*x^2 + 25*y^2 = -625 + 400
- 9*x^2 + 25*y^2 = 225
- Simplify and we get
- (x/5)^2 + (y/3)^2 = 1.
- Method 1 is simple if we understand the defintion.
- Method 2 is staightforward but the procedures are complicated.
Go to Begin
Q06. Reference
Reference
Go to Begin
