-
Q01 |
- Diagram : Ellipse in rectangular form
- Q02 | - Compare (x/5)^2 + (y/3)^2 = 1 with (x/3)^2 + (y/5)^2 = 1
- Q03 | - Find equation of directrix of (x/5)^2 + (y/3)^2 = 1
- Q04 | - Find equation of directrix of (x/3)^2 + (y/5)^2 = 1
- Q05 | - Convert (x/a)^2 + (y/b)^2 = 1 to polar form
- Q06 | - Convert (x/5)^2 + (y/3)^2 = 1 to polar form
- Q07 | - Reference
- Q02 | - Compare (x/5)^2 + (y/3)^2 = 1 with (x/3)^2 + (y/5)^2 = 1
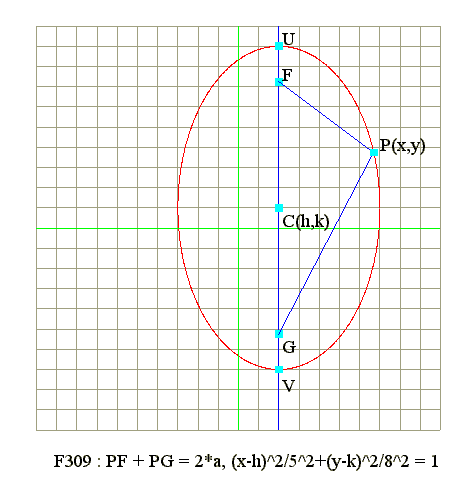
Q01. Diagram : Ellipse in rectangular form with principal axis x = k
|
Go to Begin
Q02. Compare (x/5)^2 + (y/3)^2 = 1 with (x/3)^2 + (y/5)^2 = 1
Equation (x/5)^2 + (y/3)^2 = 1
- 1. Principal axis y = 0
- 2. Semi-axese a = 5 and b = 3
- 3. Focal length f = Sqr(a^2 + b^2) = 4
- 4. Vertices U(-5, 0) and V(+5, 0)
- 5. Foci F(-4, 0) and G(4, 0)
- 6. Equation of directrix
- x = -4 - D, or
- x = +4 + D
- 7. Polar form
- R = D*e/(1 - e*cos(A)), or
- R = D*e/(1 + e*cos(A))
- 1. Principal axis x = 0
- 2. Semi-axese a = 5 and b = 3
- 3. Focal length f = Sqr(a^2 + b^2) = 4
- 4. Vertices U(0, -5) and V(0, +5)
- 5. Foci F(0, -4) and G(0, 4)
- 6. Equation of directrix
- y = -4 - D or
- y = +4 + D
- 7. Polar form
- R = D*e/(1 - e*sin(A)), or
- R = D*e/(1 + e*sin(A))
Go to Begin
Q03. Find equation of directrix of (x/5)^2 + (y/3)^2 = 1
Corresponding polar form
- 1. Focus F is origin : Left side
- R = (D*e)/(1 - e*cos(A))
- (x/a)^2 + (y/b)^2 = 1
- 2. Focus G is origin : Right hand side
- R = (D*e)/(1 + e*cos(A))
- (x/a)^2 + (y/b)^2 = 1
- FU = a - f
- R = a - f
- Angle A = 180 and R = (D*e)/(1 - e*cos(180))
- Since cos(180) = -1
- Hence (a - f) = (D*e)/(1 + e)
- Hence D = (a - f)*(1 + e)/e
- Or D*e = (a^2 - f^2)/a
- For (x/a)^2 + (y/b)^2 = 1
- Center at (0, 0)
- Focus F at (-f, 0)
- Hence equation of directrix : x = -f - D
- FV = a + f
- R = a + f
- Angle A = 0 and R = (D*e)/(1 - e*cos(0))
- Since cos(0) = 1
- Hence (a + f) = (D*e)/(1 - e)
- Hence D = (a + f)*(1 - e)/e
- Or D*e = (a^2 - f^2)/a
- For (x/a)^2 + (y/b)^2 = 1
- Center at (0, 0)
- Focus F at (-f, 0)
- Hence equation of directrix : x = -f + D
Go to Begin
Q04. Find equation of directrix of (x/3)^2 + (y/5)^2 = 1
Corresponding polar form
- 1. Focus F is origin : Left side
- R = (D*e)/(1 - e*sin(A))
- (x/3)^2 + (y/5)^2 = 1
- 2. Focus G is origin : Right hand side
- R = (D*e)/(1 + e*sin(A))
- (x/3)^2 + (y/5)^2 = 1
- FU = a - f
- R = a - f
- Angle A = 90 and R = (D*e)/(1 + e*sin(0))
- Since sin(90) = 1
- Hence (a - f) = (D*e)/(1 + e)
- Hence D = (a - f)*(1 + e)/e
- Or D*e = (a^2 - f^2)/a
- For (x/a)^2 + (y/b)^2 = 1
- Center at (0, 0)
- Focus F at (0, +f)
- Hence equation of directrix : y = f + D
- FV = a + f
- R = a + f
- Angle A = 270 and R = (D*e)/(1 + e*sin(270))
- Since sin(270) = -1
- Hence (a + f) = (D*e)/(1 - e)
- Hence D = (a + f)*(1 - e)/e
- Or D*e = (a^2 - f^2)/a
- For (x/a)^2 + (y/b)^2 = 1
- Center at (0, 0)
- Focus F at (0, -f)
- Hence equation of directrix : y = -f - D
Go to Begin
Q05. Convert (x/a)^2 + (y/b)^2 = 1 to polar form
Method 1 : Find D and e
- Corresponding form
- R = (D*e)/(1 - e*cos(A)) : The center at (f, 0)
- ((x - f)/a)^2 + (y/b)^2 = 1 : The center at (f, 0)
- (x/a)^2 + (y/b)^2 = 1 : The center at (0, 0)
- Since the translation from (0, 0) to (f, 0), the diagram is no change
- Hence we know that the polar form is R = (D*e)/(1 - e*cos(A))
- R = D*e/(1-e*cos(A))
- The focal point is at F(0, 0)
- The center is at (f, 0)
- Hence rectangular form is ((x - f)/a)^2 + (y/b)^2 = 1
- Remove denominator and simplify
- (b^2)*(x + f)^2 + (a^2)*(y^2) = (a^2)*b*2.
- (b^2)*(x^2) + (b^2)*x*f + (b^2)*(f^2) + (a^2)*(y^2) = (a^2)*(b^2)
- Since b^2 = a^2 - f^2.
- Hence (b^2)*(x^2) + (a^2)*(y^2) + 2*(b^2)*x*f = (a^2)*(b^2) - (b^2)*(f^2)
- (a^2 - f^2)*(x^2) + (a^2)*(y^2) + 2*(b^2)*x*f = (b^2)*(a^2 - f^2)
- Polar coordiantes
- x = R*cos(A)
- y = R*sin(A)
- R^2 = x^2 + y^2
- Substitute polar coordinates into above equation
- (x^2 + y^2)*(a^2) - (f^2)*(x^2) + 2*(b^2)*x*f = b^4
- (R^2)*(a^2) - (f^2)*(x^2) + 2*(b^2)*x*f - b^4 = 0
- (R^2)*(a^2) - ((f^2)*(x^2) - 2*(b^2)*x*f + b^4)
- (R^2)*(a^2) - (f*x - b^2)^2 = 0
- R*a = f*x - b^2
- Since x = R*cos(A)
- Hence R*a - R*f*cos(A) = b^2
- R*(a - f*cos(A)) = b^2
- R*(1 - f*cos(A)/a) = (b^2)/a
- Since e = f/a and D*e = (b^2)/a
- Hence R = (D*e)/(1 - e*cos(A))
Go to Begin
Q06. Convert (x/5)^2 + (y/3)^2 = 1 to polar form
Method 1 : Find D and e
- The polar form is R = (D*e)/(1 - e*cos(A))
- Since f = Sqr(a^2 - b^2) = 4
- Also D*e = (a - f)*(1 + e) = (a^2 - f^2)/a = (b^2)/a
- a = 5 and b = 3
- e = f/a = 4/5 = 0.8
- D*e = (5 - 4)*(1 + 0.8) = 1.8
- R = 1.8/(1 - 0.8*cos(A))
- Since center of R = (D*e)/(1 - e*cos(A)) is at (f, 0)
- We must use equation ((x - f)/a)^2 + (y/b)^2 = 1
- Since f = Sqr(a^2 - b^2) = 4
- Hence 9*(x - 4)^2 + 25*(y^2) = 225
- 9*(x^2) - 72*x + 9*14 + 25*(y^2) = 225
- Change coefficient of x^2 same as y^2
- 25*x^2 - 16*x^2 - 72*x + 25*(y^2) = 81
- 25*(x^2 + y^2) = 16*(x^2) + 72*x + 81
- Since R^2 = x^2 + y^2
- Hence 25*(R^2) = (4*x + 9)^2
- Take square root on both sides : 5*R = 4*x + 9
- R = 0.8*x + 1.8
- Since x = R*cos(A)
- Hence R = 0.8*R*cos(A) + 1.8
- The answer is R = 1.8/(1 - 0.8*cos(A))
Go to Begin
Q07. Reference
Reference
Go to Begin
