
Home Page
Personal Information
School Information
Reference Materials
Information for Students
Problem of the Week
Chaparral and & New Mexico
Math Tutorial
Marvelous Math Links
Odds & Ends
Games and Gadgets
Fraction Calculator
Weekly Skills Quiz
Famous Mathematicians

Visit MathStar New Mexico

Arithmetical Properties
Order of Operations
Divisibility Tests
Solving Proportions
Powers and Exponents
Prime and Composite Numbers
Greatest Common Factor
Least Common Multiple
Least Common Denominator
Pascal's Triangle
Fibonacci Numbers
Golden Ratio.
Triangular Numbers.
Percent
Signed Integers
Mathematical Series and Sequences
Changing a Fraction to a Decimal
Changing a Fraction to a Percent
Fractions
Changing Mixed Numbers to Improper Fractions
Changing Improper Fractions to Mixed Numbers
Adding Like Fractions
Adding Unlike Fractions
Subtracting Unlike Fractions
Adding Mixed Numbers With Like Fractions
Subtracting Mixed Numbers With Like Fractions
Subtracting Mixed Numbers With Unlike Fractions
Geometric Figures
Pythagoras and his theorum
More coming soon!
Concept: Powers and Exponents
Exponents are simply a shorthand way of writing repeated multiplication just as multiplication is a shorthand for repeated addition.
the notation
The notation
3x3x3x3x3=243
Concept: Triangular Numbers
A numerical quantity that may be arranged in a triangle shape, such as bowling pins or billiard balls is called a triangular number.

If you look closely it is easy to see that triangular numbers may be found by simply adding consecutive numbers.
1+2=3
1+2+3=6
1+2+3+4=10 etc.
1+2+3=6
1+2+3+4=10 etc.
Concept: Pythagorean Theorum
Pythagoras, an ancient Greek mathematician, discovered (at least he gets credit for it) an important concept concerning right triangles. He found that the sum of the squares of the two sides forming the right angle add up to the sum of the square of the hypotenuse.
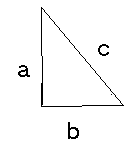
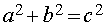
The ancient Babylonians knew of right triangles with whole number sides in fact one tablet found (Plimpton 322) contains a formula for calculating such triangles. In modern terms it is written as
Where m is any whole number.
Concept: Golden Ratio
The Golden Ratio is a concept developed by the ancient Greek mathematicians. It seems to have a strong connection with human perceptions since if you ask people to draw a rectangle most will draw a rectangle with sides in a ratio of 1 to 1.618.
People seem to find this ratio pleasing. Architects take advantage of it, incorporating this shape into buildings. Artists use it to lay out there works and so on.
Its value is about 1.618034.
Look at the Links page for much more information on
the Golden Ratio.
Concept: Fibonacci Numbers
Fibonacci lived about 1200 A.D. One of the greatest mathematicians of the middle ages, he became interested a particular series of numbers that have since found great importance.
The numbers are easily found by starting with a pair of 1's and adding the last two numbers to get each new member of the series.
1, 1, 2
The 2 is found by adding the 1 and 1. the next number is found by adding the last two.
1+2 = 3 and we have 1, 1, 2, 3
Continuing this pattern we have
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
For the Fibonacci series.
If you divide two terms that are adjacent, (smaller into larger) you will find that as you use larger and larger numbers the answer seems to get closer and closer to some particular value.
The value that these answers are getting close to is known as the Golden Ratio.
Look at the Links page for much more information on
Fibonacci!
Concept: Percent
Percent comes from a Latin word 'percentum' where per means divide and centum means 100. (There are 100 years in a century and 100 cents in a dollar aren't there!)
That's all it means - divide by 100. Therefore 30% just means
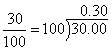
Concept: Solving Proportions
A proportion is simply an equality between two ratios.

Often a number is missing which we need to find. For example,
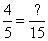
Start by drawing a large x through the problem as shown:
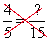
Find two numbers that are on the same line. In this case the 4 and 15. Multiply these numbers.
4x15=60
Find the number that is on the same line as the missing number. In this case the 5. Divide your product by this number.
60 ÷ 5 = 12
Replacing the '?' with this number we find that
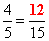
It does not matter which of the four numbers is missing. These same steps will always find the missing number.
Concept: Geometric Figures
Line Segment: A line segment is a portion or part of a line.
Right Angle: A right angle contains 90 degrees and forms a square corner.
Triangle: A triangle is a figure with three sides that are line segments and three angles.
Right Triangle: A right triangle is a triangle that contains one right angle.
Acute Triangle: An acute triangle is a triangle in which all three angles are less than 90 degrees.
Obtuse Triangle: An obtuse triangle is a triangle with one angle greater than 90 degrees.
Quadrilateral: A quadrilateral is a figure with four sides made of line segments.
Rectangle:
Concept: Arithmetical properties
Commutative Property of Addition:Changing the order of addends does not change the sum. 2+3=3+2
Commutative Property of Multiplication: Changing the order of the multiplicands does not change the product. 2x3=3x2
Associative Property of Addition: Addends may be grouped in various ways without altering the sum. 2+(3+4)=(2+3)+4
Associative Property of Multiplication:
Multiplicands may be grouped in any order without altering the product.
2x(3x4)=(2x3)x4.
Identity Property of Addition:
Any number added to 0 will remain the same. 2+0=2
Identity Property of Multiplication:
Any number multiplied by 1 will remain the same. 2x1=2
Distributive Property:
A number may be distributed inside a parenthesis without altering the result.
2x(3+4) = 2x3+2x4
Concept: Pascal's Triangle
Pascal's triangle is an array of numbers in a triangle shape in which each entry is found by adding up the two entries above it.

In the above the the 2 is found by adding the 1 and 1 above it. The 6 is found by adding the 3 and 3 above it and so on.
Check out the pascal page on this site for further information.
Concept: Order of operations
When attempting to solve problems that see simple people often get different answers. Look at the problem below.16 + 8 ÷ 2 = ?
Suppose we add 8 to the 16 getting 24 and then divide by 2. This results in an answer of 12. BUT! we could also do the division first ( 8 ÷ 2 = 4) getting four and then adding 4 to the 16 gives an answer of 20. Clearly both answers can not be correct.
To avoid this type of problem it has been decided that problems like this must be solved by doing things in a certain order. The order chosen is very simple and is listed below.
Multiplication
Division
Addition
Subtraction
This means the answer should be 20 and not the 12 arrived at by the first method above.
NOTE: It is customary to do the multiplications and divisions from left to right in the order you read them in. So in 2 x 8 ÷ by 4 we would normally multiply the 2 and 8 getting 16 and then divide this by the 4 getting 4 for the answer.
Example: 13 + 5 ÷ 6 = ? Step 1 13 + 5 = 18 Step 2 18 ÷ 6 = 3
Example: 2 x 6 - 3 = ? Step 1 2 x 6 = 12 Step 2 12 - 3 = 9
It is very easy to remember the order if you just remember the below phrase.
My Dear Aunt Sally
Multiply Divide Add Subtract
The only problem left is what to do with parenthesis or other signs of grouping.
In this case you simply start with the parenthesis, do what is inside first to eliminate them and then continue on with what is left.
Example: (22 - 7) ÷ 5 = ?
Do the 22 - 7 first getting 15. Then divide by 5 to get 3 for your answer.
Keep in mind there are lots of different ways to indicate multiplication in mathematics.
5 x 3 =
5 · 3 = ?
(5)(3) = ?
5(3) = ?
5[3] = ?
5{3} = ?
Concept: Divisibility Tests
Divisibility by 2:A number that ends with a 0, 2, 4, 6, or 8 (an even number) may be evenly divided by 2.
Example: 46, 10002, 57898, 1234567890
Divisibility by 3:
Add up all the digits of the number. If 3 goes into this total evenly then it will go into the original number evenly.
Example: 123 ( 1+2+3=6), 471 (4+7+1=12), 1113 (1+1+1+3=6)
Divisibility by 4:
Divide 4 into the last 2 digits of the number. if it goes evenly then it will go into the original number evenly.
Example: 312 ( 12÷ 4=3), 769920 (20 ÷ 4 = 5)
Divisibility by 5:
If the number ends with a 5 or a 0, it is evenly divisible by 5.
Example: 1111115, 12345, 9997775, 811110
Divisibility by 6:
Check for both 2 and 3. If they both work, then the number may be divided by 6 evenly.
Divisibility by 7:
Sorry but the rule is more difficult that actually doing the division!
Divisibility by 8: Divide 8 into the last three digits of the number. If it goes evenly then it will go into the entire number evenly.
Example: 1008, ( 008 ÷ 8 =1), 45128 (128 ÷ 8 = 16)
Divisibility by 9:
Add up the digits. If 9 goes into the sum evenly it will go into the number evenly.
Example: 711 (7+1+1 = 9), 7434 (7+4+3+4=18)
Divisibility by 10:
The number ends with a 0.
Example: 340, 580, 11111111111110
Divisibility by 11:
Start with the far left digit of the number and add up every other digit to get a sum. Go back and add the digits you skipped to get a second sum. Subtract the smaller sum from the larger sum. If you get 0 or a multiple of 11 then the number may be divided by 11.
Example: 352 (3 + 2=5 and 5=5, the difference is 0), 7931 (7+3=10 and 9+1=10, the difference is 0)
Concept: Prime and Composite Numbers
Factor: A factor of a number is another number that divides evenly into the first number. For example 5 is a factor of 35 since 5 divides evenly into 35.
Prime Number: has only two factors, 1 and the number itself. For example 13 is a prime number since the only factors are 1 and 13.
Composite Number: A composite number has at least three factors. For example 6 is composite since 1, 2, 3, and 6 will all divide evenly into it.
To find out whether a number is prime or composite you may try the divisibility tests shown above.
Concept: Greatest Common Factor
The greatest common factor is the largest factor that two or more numbers have in common. All numbers have 1 as a factor but often there is a larger common factor also.
One method of finding the greatest common factor (GCF) is simply to list the factors or the numbers and pick out the largest.
Example: 18 and 24. 18 has factors of 1, 2, 3, 6, and 9 - 24 has factors of 1, 2, 3, 4, 6, and 12. The largest factor they share in common is 6 so it is the GCF of 18 and 24.
A second method is to list all the prime factors of both numbers. Circle the prime factors they have in common. Multiply one of each pair of factors circled to find the GCF.
Example: 18 and 21. The prime factors of 18 are 1, 2, and 3. the prime factors of 21 are 1, 3, and 7. The common factors are 1, and 3. Multiply them to get 3 for the GCF.
Example: 24 and 36. 24 = 1 x 2 x 2 x 2 x 3 and 36 = 1 x 2 x 2 x 3 x 3. They share factors of 1, 2, 2, and 3. Multiplying these (1 x 2 x 2 x 3 = 12) we find the GCF is 12.
Concept: Least Common Multiple
The smallest non-zero multiple of two or more numbers is called the Least Common Multiple or LCM.
One method of finding it is to list the multiples of all the numbers until you find one in common.
Example: 6 and 9, 6 has multiples 6, 12, 18, 24, 30, 36, 42 etc. While 9 has multiples of 9, 18, 27, 36, 45 etc. It is easy to see that 36 is a multiple of both 6 and 9 and it is the smallest such multiple.
A second way uses prime factors. List all the prime factors of your numbers. Pick each factor the most number of times it was used as a factor. If 2 was used 1 time in the first number but 2 times in the second number you would use it as a factor 2 times.
Example: 6 and 9. 6 has prime factors of 1, 2, and 3 while 9 has prime factors of 1, 3, and 3. To find the LCM we would use 1, one time, 2 one time but we would use 3 twice since that is the most number of times it was used as a factor in either number. Thus the LCM is 1 x 2 x 3 x 3 = 18.
Example: 12 and 18. 12 = 1 x 2 x 2 x 3. 18 = 1 x 2 x 3 x 3.
The LCM = 1 x 2 x 2 x 3 x 3 = 36
Concept: Mathematical Sequences and Series
A mathematical sequence is a series of numbers or other items where each is related to the others by some mathematical rule.
A simple example is the sequence of natural numbers. 1, 2, 3, 4, 5, ... Where each member of the sequence is one larger than the member before it.
Another simple example is the sequence 1, 3, 5, 7, ... Where each member is 2 more than the preceding member.
A more difficult example would be 2, 5, 14, 41, ... Where each member is found by multiplying the preceding member by three and then subtracting 1 from the product.
Sequences such as this are a bit more difficult to figure out by they are very common. This sort of rule is the first thing one should look for. Remember you might multiply and then either add or subtract something.
One sequence that does follow a different pattern is the Fibonacci sequence, named after a mathematician who lived around the year 1200.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ..
.Did you notice that each number is found by adding the preceding two members? This unusual sequence has many important properties.
See the Fibonacci page on this site to find out more information.
Another sequence is 1, 2, 4, 7, 11, 16, 22, ...
In this one the second number is 1 more than the first, the third number is 2 more than the second, while the fourth number is 3 more than the third and so on. Sometimes you need to look closely to see how the sequence is formed.
Concept: Least Common Denominator
The Least Common Denominator (LCD) is simple the least common multiple of the denominators of two or more fractions.
Example: If we have fractions of 5/6 and 4/9, we can find the LCD easily. 6 = 1 x 2 x 3 and 9 = 1 x 3 x 3. taking each factor the most number of times it is used we have LCD = 1 x 2 x 3 x 3 = 18.
Concept: Signed Inegers
Signed Integers are simply integers with a + or - sign attached.Adding Signed Integers:
If the signs are the same you add and give the answer the common sign.
+2+(+3) = +5
-2+(-2) = -5 If the signs are different, subtract the smaller from the larger and give the answer the same sign as the larger addend.
+2+(-3) = -1]
-2+(+3) = +1
Subtracting Signed Integers:
To subtract signed integers simply change the sign of the number immediately after the subtraction sign and follow the rule for addition. +2-( +3) = +2 + (-3) = -1
Multiplication of Signed Integers:
If the signs are the same, the answer is positive. +2x(+3)=+5, -2x(-3)=+5
If the signs are different, the answer is negative. +2x(-3) = -5, -2x(+3) = -5
Division of Signed Integers:
The rule for division is the same as multiplication, if the signs are the same, the answer is positive, if the signs are different the answer is negative.
+6 ÷ (+3) = +2, -6 ÷ (-3) = +2
+6 ÷ (-3) = -2, -6 ÷ (+3) = -2
Concept: Changing Fractions to Decimals
To change a fraction to a decimal simply divide the denominator (bottom number) into the numerator (top number).
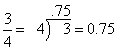
Concept: Changing a Fraction to a Percent
Remember that a percent is nothing more than a special fraction, one with a denominator or 100!
Start by setting the problem up as a proportion as shown. src="fraction2percent.gif" alt="fraction2percent.gif" align="middle">
Solve the proportion by multiplying the two numbers in opposite corners and dividing by the number in the corner opposite the '?'.
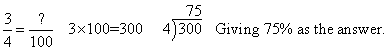
Concept: Fractions
First some definitions that are needed.
Like Fractions are fractions that have the same denominators.
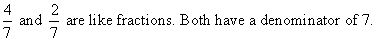
Unlike Fractions are fractions with different denominators.
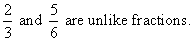
Improper Fractions are fractions in which the numerator is larger than the denominator.
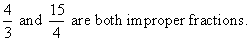
Mixed Numbers contain a whole number and a fraction part.
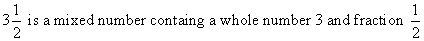
Concept: Changing Mixed Numbers to Fractions
Multiply the whole number times the denominator and add the numerator to this sum. Place this new sum over the original denominator. For Example:
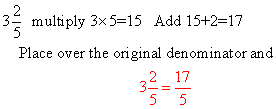
Concept: Changing Improper Fractions to Mixed Numbers
Divide the numerator by the denominator. If there is a remainder write it over the original denominator.

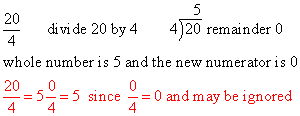
Concept: Adding like Fractions
Add the numerators. Place this sum over the original denominator. Change to a mixed number and reduce as needed.
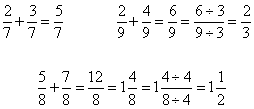
Concept: Subtracting Like Fractions
Subtract the numerators and place the difference over the same denominator.
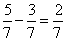
Concept: Adding Unlike Fractions
Find a common denominator for the fractions. It is the LCM of the denominators.

Next change the fractions to equivalents using the common denominator.

Next add the numerators and place the sum over the common denominator. Last, properly reduce and express the answer.
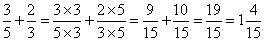
Concept: Subtracting Unlike Fractions
Subtracting unlike fractions is done the same as adding except that you subtract the numerators rather than add them.

Concept: Adding Mixed Numbers with Like Fractions
Add the Fractions first.
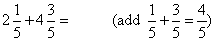
Now add the whole numbers. ( 2+4=6)
Combine the fraction and whole number parts.

Concept: Adding Mixed Numbers with Unlike Fractions:
Concept: Adding Mixed Numbers with Unlike Fractions
These are done the same as adding with like fractions except that you must first change the fraction parts so that they have a common denominator.
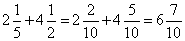
Concept: Subtracting Mixed Numbers with Like Fractions
Concept: Subtracting Mixed Numbers with Unlike Fractions
Copyright © 2000 by D. A.
Miller